Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно , а легковым автомобилем - на весь путь время затрачено часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений
Умножив левую и правую части уравнения на 3x(x+12) ≠ 0.
чтобы найти х, в которых функции пересекаются, нужно их приравнять
sinx= корень из 3сosx
sinx- корень из 3cosx=0
возводим в квадрат, чтоб избавиться от корня.
sin^2x-3cosx=0
заменяем sin^2x на 1-cos^2x ( из основного тригонометрического тождества)
-cos^2x-3cosx+1=0
делим на минус
cos^2x+3cosx-1=0
замена. t=cosx
t^2+3t-1=0
D=b^2-4ac=9+4=13
t1=-3+корень из 13/2 или t2=-3-корень из 13/2
обратная замена
cosx=-3+корень из 13/2 ( больше 1, нет решений)
cosx=-3-корень из 13/2 (меньше -1, нет решений
графики функций не пересекаются
Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно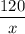
, а легковым автомобилем - 
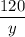на весь путь время затрачено 
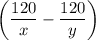часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений
Умножив левую и правую части уравнения на 3x(x+12) ≠ 0.
По теореме Виета
Скорость легкового автомобиля: 60 + 12 = 72 км/ч.
ответ: 60 км/ч и 72 км/ч.