На декартовой системе координат рисуете асимптоты 0, pi, 2pi ..., -pi, -2pi ... (как на рисунке с графиком катангенса - вертикальные пунктирные прямые к которым стремятся ост катангенса)
график функции ctg x = 1 => x=45(pi/4)- множество точек на всех интервалах(по 1 на каждом) интервалов напр. (0;pi), (pi;2pi),(2pi;3pi) ...,(-pi;0), (-2pi;-pi),(-3pi;-2pi).... для каждого интервала получаем свой х х=pi/4+pi*n у=1, где n целое , pi=3.14 т.е (pi/4;1), (pi/4+pi;1), (pi/4+2pi;1) .... (pi/4-pi;1), (pi/4-2pi;1)
На декартовой системе координат рисуете асимптоты 0, pi, 2pi ..., -pi, -2pi ...
(как на рисунке с графиком катангенса - вертикальные пунктирные прямые к которым стремятся ост катангенса)
график функции ctg x = 1 => x=45(pi/4)- множество точек на всех интервалах(по 1 на каждом) интервалов напр. (0;pi), (pi;2pi),(2pi;3pi) ...,(-pi;0), (-2pi;-pi),(-3pi;-2pi).... для каждого интервала получаем свой х х=pi/4+pi*n у=1, где n целое , pi=3.14
т.е (pi/4;1), (pi/4+pi;1), (pi/4+2pi;1) .... (pi/4-pi;1), (pi/4-2pi;1)
ctg x = корень 3/3=1/корень 3
аналогично х=pi/3 +pi*n, у=корень 3/3
ctg x = - корень 3/3
аналогично х=2pi/3 +pi*n, у=- корень 3/3
ctg x = 0
аналогично х=pi/2 +pi*n, у=0
Если число является членом арифметической прогрессии то справедливо равенство:
Подставим,проверим...
1)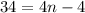
То есть n не является элементом кольца натуральных чисел,значит 34 не член прогрессии.
2)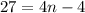
То есть n не является элементом кольца натуральных чисел,значит 27 не член прогрессии.
3)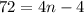
То есть n является элементом кольца натуральных чисел,значит 72 член прогрессии.
4)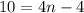
То есть n не является элементом кольца натуральных чисел,значит 10 не член прогрессии.
ответ:1)не является,2)не является,3)является,4)не является