1. Известно, что М = {а; b; d; f}, N = {b; d; е}
А) Найти М \ N
Б) N \ M
2. Найти множество истинности предложения.
n – натуральный делитель числа 8.
3. Записать уравнение:
окружности с центром в точке А(–3,2; 1) и радиусом r = 4.
4. Записать уравнение:
прямой, проходящей через точки М(0; 4); N(–2; 0).
5. Среди прямых, заданных уравнениями 3х + у = 2, –2х + у = 3,
, 4х – 2у = 1, указать те, которые пересекают прямую 2х – у = 1.

Вычтем из первого уравнения системы второе:

Если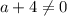 , то в силу того, что произведение равно нолю,  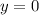. И, подставляя это, например, во второе уравнение, имеем:

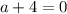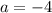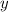Значит, чтобы решений было бесконечно много, нужно чтобы или же . При этом значении переменная может быть любым числом. И каждому значению переменной соответствует свое значение переменной .

Действительно, в этом случае первое и второе уравнение системы будут совпадать с точностью до умножения на два:

Задача решена!

а) х(х+11)-8>4x                                                    

x²+11x-8>4x                                                            

x²+11-8-4x>0                                                          

x²-4x+3>0                                                                

x²-4x+3=0                                                                                                                                

D=b²-4ac=16-4*3=16-12=4                                      

x1,2=-b±√D/2a                                                                                                            

x1=4+2/2=3

x2=4-2/2=1

Розлаживаем множители по формуле

a(x-x1)(x-x2)=(x-3)(x-1)

x∈(-∞;1)∪(3;+∞)

Объяснение: