График параболы в общем случае выглядит следующим образом:
y = ax² + bx + c, где a,b,c = const
Так как парабола проходит через начало координат её уравнение примет вид:
y = ax²
Подставим координаты точки B и найдём значение коэффициента а.
y = -0,25x² - уравнение искомой параболы
Найдём пересечение с прямой y = -16
-16 = -0,25x²
x² = 64
x = ±8
Координаты пересечения: (8, -16) и (-8, -16)
Пусть общий вид уравнения параболы , но так как вершина параболы находится в начале координат, то уравнение параболы имеет вид:
Функция проходит через точку B(-1; -1/4), тогда, подставляя координаты точки в функцию, получаем:
Таким образом, искомое уравнение параболы
Осталось вычислить в каких точках функция пересекает прямую y = -16, для этого просто напросто приравниваем функции, получаем:
Графики пересекаются в точках (-8; -16) и (8; -16).
График параболы в общем случае выглядит следующим образом:
y = ax² + bx + c, где a,b,c = const
Так как парабола проходит через начало координат её уравнение примет вид:
y = ax²
Подставим координаты точки B и найдём значение коэффициента а.
y = -0,25x² - уравнение искомой параболы
Найдём пересечение с прямой y = -16
-16 = -0,25x²
x² = 64
x = ±8
Координаты пересечения: (8, -16) и (-8, -16)
Пусть общий вид уравнения параболы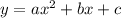 , но так как вершина параболы находится в начале координат, то уравнение параболы имеет вид:
, но так как вершина параболы находится в начале координат, то уравнение параболы имеет вид:
Функция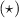 проходит через точку B(-1; -1/4), тогда, подставляя координаты точки в функцию, получаем:
проходит через точку B(-1; -1/4), тогда, подставляя координаты точки в функцию, получаем:
Таким образом, искомое уравнение параболы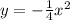
Осталось вычислить в каких точках функция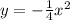 пересекает прямую y = -16, для этого просто напросто приравниваем функции, получаем:
пересекает прямую y = -16, для этого просто напросто приравниваем функции, получаем:
Графики пересекаются в точках (-8; -16) и (8; -16).