1.Найди корень уравнения 16x+11=0 .

a) −1,81
б) Бесконечно много решений
в) x∈∅
г) Нет верного ответа

2.При каких значениях a сумма дробей 3a+2a и 2a−12a равна 1?

(Не выделяй целую часть.)

ответ: a=

3.Реши уравнение:

2x+2−104−x2+1=1x−2 .

Выбери область определения данного дробного уравнения:
D=R\{−2}
D=R{0}
D=R
D=R\{2}
D=R\{−2;2}
D∈∅

Выбери корни (корень) данного дробного уравнения:
x=−1
x=1
x=0;x=−1
x∈(0;1)
x=0
x∈R
x∈∅

4.Реши уравнение 7x−5x+6=0.
x=

Дополнительный во при каких значениях переменной уравнение не имеет смысла?

(Первым пиши меньшее значение).

a) Возрастает: (-∞;0)∪(2/3;∞), убывает: (0;2/3)

б) 0 - локальный максимум, 2/3 - минимум

в) Наибольшее y=52 при x=4, наименьшее: y=4 при x=1

Объяснение:

Производная равна: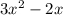 . Отсюда x1=0, x2=2/3. Это точки экстремума.

б)

0 - максимум

2/3 - минимум

а)

На основании максимума и минимума получаем:

Функция возрастает (-∞;0)∪(2/3;∞)

Функция убывает (0;2/3)

в)

На всем промежутке от 1 до 4 функция возрастает, поэтому наименьшее значение y=4 находится при x=1, а наибольшее y=52 находится при x=4.

Нужно просто подставить 1 и 4 в функцию вместо x, чтобы вычислить y.

Чтобы найти скорость грузовика в гору, мы можем использовать простое уравнение. Общее время в пути 9 часов, а общее расстояние 300 км, из них 120 км по равнине и 180 км в гору. Это означает, что грузовик провел 6 часов (2/3 всего времени) на подъеме и 3 часа (1/3 всего времени) на ровном участке. Так как скорость подъема грузовика на 25% меньше, чем его скорость по ровной местности, мы можем рассчитать скорость подъема в гору, умножив скорость по ровной дороге на 0,75. Если мы предположим, что скорость грузовика по ровной дороге составляет 90 км/ч, то скорость на подъеме составит 0,75 х 90 = 67,5 км/ч.