1. Найдите наименьший угол треугольника, стороны которого равны 14 см, 16 см и 18 см. ответ дайте в градусах, округлив до целых
2. Расстояние между точками А и В равно 180 м. Дом на противоположном берегу реки видно из точки А под углом 45°, а из точки В под углом в 15°. Вычислите расстояние от дома до точки В.
3.
Впишите правильный ответ.
В равнобедренной трапеции АВСD боковая сторона СD равна 10, а основания равны 3 и 15. Найдите длины диагоналей трапеции. ответ запишите в виде десятичных дробей, округлив их до десятых.

0,4

Объяснение:

Пронумерую места на скамейке от 1 до 5, нумерация слева направо. Общее число вариантов рассадки относительно этих мест = 5! = 5*4*3*2*1 = 120 (на первое место могут сесть 5 человек, на второе - 4, т.к. кто-то уже сидит, и т.д.).

Пусть первая девочка сидит левее второй. Тогда если они сидят вместе, то на местах соответственно: 1 и 2, 2 и 3, 3 и 4, 4 и 5 - 4 варианта. Для каждого варианта есть 3! = 6 вариантов рассадки мальчиков (девочки зафиксированы на своих местах). Тогда суммарно в этом случае будет 4*6 = 24 подходящих случая. Если они поменяются местами - это ещё 24 варианта, итого 48 нужных вариантов из 120, т.е. вероятность равна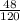 = 0,4.

149,6 м

Объяснение:

a - сторона квадратного зала, м.

(a+5) - длина прямоугольного зала, м.

(a+3) - ширина прямоугольного зала, м.

(a+5)(a+3)=1,6a²

1,6a²-a²-3a-5a-15=0

0,6a²-8a-15=0; D=64+36=100

a₁=(8-10)/1,2=-5/3 - этот корень не подходит ро смыслу задачи.

a₂=(8+10)/1,2=30/2=15 м - сторона квадрата.

15+5=20 м - длина прямоугольника.

15+3=18 м - ширина прямоугольника.

Периметр прямоугольного зала:

P₁=2(18+20)=2·38=76 м

Периметр квадратного зала:

P₂=4·15=60 м

Необходимое количество плинтусов для ремонта двух залов:

((76+60) ·(100%+10%))/100%=(136·11)/10=149,6 м.