1) найдите тангенс угла наклона к оси абсцисс касательной проходящей через точку м графика функции f f(x)=0,5x^2+x m(3; 8)2) найдите угловой коэффициент касательной (k), проведённой к графику функции f в точке с абсциссой x₀f(x)=2cosx+43) найдите координаты точек графика функции в которых касательная параллельна оси абсцисс (0x) f(x)=1/2x^4+16x4) дана функция f(x)=3+7x-4x^2 найти координаты точки графика в которойугловой коэффициент касательной равен -9
1) 1-3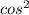
x=2sin(x)cos(x)
единицу представим по тригонометрическому тождеству:1=sin²x+cos²x
sin²x+cos²x-3cos²x-2sin(x)cos(x)=0
sin²x-2sin(x)cos(x)-2cos²x=0
делим каждый член уравнения на cos²x
tg²x-2tgx-2=0
решаем квадратное уравнение
D=12
tgx₁=1+√3 tgx₂=1-√3
x₁=arctg(1+√3)+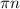
x₂=arctg(1-√3)+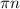
2) 3Sin²x+2SinxCosx=2
3Sin²x+2SinxCosx=2(Sin²x+Cos²x)
Sin²x+2SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим его на Cos²x
Tg²x+2Tgx-2=0
Tgx=y
y²+2y-2=0
D=12>0
y=(-2+2√3)/2=-1+√3 или y=(-2-2√3)/2= -1-√3
Tgx=-1+√3⇒ x=arctg(-1+√3)+πn,n∈Z
Tgx= -1-√3 ⇒x= arctg(-1-√3)+πn,n∈Z
Объяснение:
1)
В лифт 9-этажного дома на первом этаже зашли 6 человек. Найти вероятность того, что все выдут на разных этажах, если каждый с одинаковой вероятностью может выйти на любом этаже, начиная со второго.
Рассуждаем так. Чтобы пассажиры вышли на разных этажах нужно лифту остановится 6 раз на любом из 8 этажей. (на 2,3,4,5,6,7,8,9) Тогда общее число исходов событий
теперь каждый может выйти только на одном этаже.. при этом второй уже этот этаж должен проехать
Значит число возможных исходов
8*7*6*5*4*3=20160
тогда вероятность 20160/262144= 0,0769
2)
сколькими можно разделить группу из 17 человек на две группы чтобы в одной было 5 человек , а в другой 12 ?
Тут все проще.. Если мы выберем группу из 5 человек то остальные попадут во вторую группу.. Значит достаточно просто посчитать количество возможных выбрать группу 5 человек из 17