1.Найти первые пять членов арифметической прогрессии, в которой a1= - 5; d= 5
-5;0;5;10;15;
2.Найти первые шесть членов арифметической прогрессии, если a1=5; d= -3.
3. Найти разность арифметической прогрессии, в которой a10=16; a18=24
4) Вычислить сумму девяти первых членов арифметической прогрессии, в которой a1=15; d = -4
5) Найти двадцать пятый член арифметической прогрессии 3;6;…
6. Арифметическая прогрессия задана формулой cn=13n-67. Найдите первый положительный член прогрессии
7) { an}- арифметическая прогрессия, у которой a14=4,7; d=0,8.Найти a1 и a19
8) Найдите двадцать первый член арифметической прогрессии, если a3=12,4; a13= - 21,6

Объяснение:

6g66yggyy6y6yygyygg6ygggfy6yyy6gyyĝg6gyyyĝyyĝyyyg6yyĝggĝ GG ĝĝĝfĝggĝxĝgff GG GG your g GG GG of fg fg f GG GG GG good ft Lauderdale GG ggg GG g GG ĝfg GG g ft g GG g GG fggf ĝĝĝfĝggĝxĝgff ggyfgg ft fggf ĝĝĝfĝggĝxĝgff xgg GG gg GG g GG fggf GG ffg GG GG g GG f, TX for ZDPCWQ yyygyyggg ggyfgg y GG you get ygg yyygyyggg to ggyfgg g GG yy GG gyygy yyygyyggg GG yyy gy yggygyygygggy GG GG GG gyg GG fyyy GG GG GG y g GG f ft yyf yyg GG GG GG gg GG GG GG GG gg GG gy gyg ygg yyygyyggg gy GG GG GG g GG gygggy GG gy fggf g yyygyyggg ggy gy gg ĝ yyygyyggg ggyfgg ggyfgg g ft fggf gg GG y xxyxyzyd

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .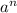

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .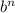

Рассмотрим многочлен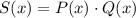 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :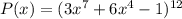

- степень определяется выражением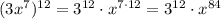 , то есть степень равна 84

- свободный член равен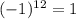

Для многочлена :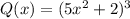

- степень определяется выражением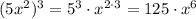 , то есть степень равна 6

- свободный член равен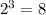

Наконец, для многочлена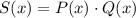 получим:

- степень определяется выражением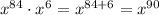 , то есть степень равна 90

- свободный член равен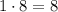

Сумма степени и свободного члена многочлена :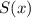

ответ: 98