1) найти y'(2), если у = (х + 5) ln x

2) найти у'(2), если у = lnx/x

Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).

Это координаты вершины, почему именно такие? Корни уравнения:

, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.

Найдём нули функции:

Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.

И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: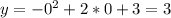 то есть (0;3)

1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения

При x∈(-1;3) функция принимает положительные значения

2) При x∈(-∞;1) функция растёт

При x∈(1;+∞) функция убывает

3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)

Максимальное значение 4, достигается в точке (1;4)

вспомним что такое модуль

|x| = x  x>=0

    = -x  x<0

Пишем на всякий случай ОДЗ x≠3 и смотрим подмодульное выражение

(x²+x-2)/(x-3) = (x+2)(x-1)/(x-3)

D=1+8 = 9

x12=(-1+-3)/2 = -2 1

смотрим метод интервалов

[-2] [1] (3)

Итак при

1. x∈[-2 1) U (3 + ∞)

|(x²+x-2)/(x-3)| = (x²+x-2)/(x-3)

2. x∈(-∞-2) U [1  3)

|(x²+x-2)/(x-3)| = - (x²+x-2)/(x-3)

решаем полученные уравнения

1. x∈[-2 1] U (3 + ∞)

(x²+x-2)/(x-3) = (x²+x-2)/(x-3) решения все числа на интервалах с учетом одз

x∈[-2 1) U (3 + ∞)

2. x∈(-∞-2) U (1  3)

(x²+x-2)/(x-3) = - (x²+x-2)/(x-3)

2(x²+x-2)/(x-3) = 0

x=1  x=-2 решений нет

ответ x∈[-2 1] U (3 + ∞)