1) область определения функции; 2) область значений функции;
3) четность, нечетность функции, периодичность (обсудите это понятие);
4) нули функции (с осью Ох); точки пересечения с осью Оу
5) промежутки знакопостоянства функции;
6) промежутки монотонности функции (возрастание, убывание);
7) непрерывность функции;
8) экстремумы функции;

1) область определения функции; 2) область значений функции;3) четность, нечетность функции, периоди

Показать ответ

Ответ:

nastasyasaenko

02.01.2023 00:23

ответ: 64 и 96 км/час.

Объяснение: формула известна: путь = скорость * время;

до встречи автомобили двигались с разной (видимо) скоростью - обозначим (х) км/час для автомобиля из А->В и (у) км/час для автомобиля из В->А, значит разное расстояние - (х*t) км и (у*t) км, одинаковым было время (в пути до встречи), обозначим (t) часов.

x*t + y*t = 80 (км)

оставшуюся часть пути (это у*t) автомобиль из А->В со скоростью (х) за 45 минут = 3/4 часа: y*t = (3/4)*x

t = 3x / (4y)

оставшуюся часть пути (это x*t) автомобиль из со скоростью (y) за 20 минут = 1/3 часа: x*t = (1/3)*y

t = y / (3x)

получим: 3x / (4y) = y / (3x)

9x^2 = 4y^2 ---> 3x = 2y

y = 1.5x (т.е. скорость одного авто в 1.5 раза больше скорости другого)

(y/3) + (3x/4) = 80

4*1.5х + 9x = 80*12

15x = 5*16*4*3

x = 16*4 = 64 (км/час)

у = 1.5*64 = 3*32 = 96 (км/час)

Проверка:

из А->В автомобиль со скоростью 64 км/час за 80/64 часа = 5/4 часа = 1 час 15 минут

из В->А автомобиль со скоростью 96 км/час за 80/96 часа = 5/6 часа = 50 минут

тогда

из А->В автомобиль до встречи за 1 час 15 минут - 45 минут = 30 минут

из В->А автомобиль до встречи за 50 минут - 20 минут = 30 минут

0,0(0 оценок)

Ответ:

Lizzkkaa

09.04.2022 08:27

Наш многочлен имеет вид

P(x)=ax^4+bx^3+cx^2+dx+e

Пусть меньший его корень равен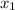 x_1 . Так как корни образуют арифметичекую прогрессию, можем записать:

$x_2=x_1+1\\x_3=x_1+2\\x_4=x_1+3$

Многочлен раскладывается на линейный множители следующим образом:

P(x)=a(x-x_1)(x-x_1-1)(x-x_1-2)(x-x_1-3)

Напрашивается замена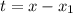 t=x-x_1 . Тогда

P(t)=at(t-1)(t-2)(t-3)=a(t^4-6t^3+11t^2-6t)

Нам нужно найти минимумы этой функции, поэтому дифференцируем:

P'(t)=a(4t^3-18t^2+22t-6)

Теперь требуется найти корни этого многочлена. Используя теорему о рациональных корнях многочлена можно найти корень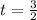 $t=\frac{3}{2}$

Согласно теореме Безу,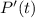 P'(t) должен делиться на 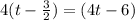$4(t-\frac{3}{2} )=(4t-6)$ . Разложим на множители, чтобы найти остальные корни:

P'(t)=a(4t^3-6t^2-12t^2+18t+4t-6)=a[t^2(4t-6)-3t(4t-6)+(4t-6)]=a(4t-6)(t^2-3t+1)

Решив квадратное уравнение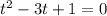 t^2-3t+1=0 , найдем корни

$t_{1, 2}=\frac{3\pm\sqrt{5} }{2}$

Расположив корни

$\frac{3}{2},\;\frac{3\pm\sqrt{5} }{2}$

на числовой прямой и использовав метод интервалов, узнаем, что производная меняет знак с минуса на плюс в точках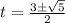 $t=\frac{3\pm\sqrt{5} }{2}$ , это и есть точки минимума. Переходя обратно к многочлену от x, получаем точки