A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.
Б) Не верно. Верна формула
В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.
Б) Не верно. Верна формула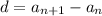
В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
x+y+xy=11 x+y=11-xy (x+y)²=121-22xy+(xy)²
x²+xy+y²=19 x²+2xy+y²=19+xy (x+y)²=19+xy ⇒
121-22xy+(xy)²=19+xy
(xy)²-23xy+102=0
Пусть ху=t ⇒
t²-23t+102=0 D=121 √D=11
1) t₁=xy=6 ⇒
x+y+6=11 x+y=5 y=5-x
x²+6+(5-x)²=19
x²+6+25-10x+x²-19=0
2x²-10x+12=0 |÷2
x²-5x+6=0 D=1
x₁=2 y₁=5-2=3
x₂=3 y₂=5-3=2.
2) t₂=xy=17 ⇒
x+y+17=11 x+y=-6 y=-x-6=-(x+6).
x²+17+(-(x+6))²=19
x²+17+x²+12x+36-19=0
2x²+12x+34=0 |÷2
x²+6x+17=0 D=-32 ⇒ Уравнение не имеет действительных корней.
ответ: x₁=2 y₁=3 x₂=3 y₂=2.