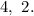1. По графику функции определить: а) область определения функции;
б) область значений функции;
в) промежутки возрастания функции;
г) промежутки убывания функции;
д) нули функции;
е) промежутки, на которых функция принимает положительные значения;
ж) промежутки, на которых функция принимает отрицательные значения;
3) наибольшее и наименьшее значение функции

1. По графику функции определить: а) область определения функции;б) область значений функции;в) пром

Показать ответ

Ответ:

filltema

01.03.2021 14:57

Объяснение:

$\displaystyle (2 {sin}^{2} (x) - 3 \cos(x) ) \times \sqrt{ \tan(x) } = 0$

а)ОДЗ:

{ tan(x) ≥0 (Т.к. подкоренное выражение всегда неотрицательно)

{ cos(x) ≠0 (Т.к. тангенс это синус, делённый на косинус,а на ноль делить нельзя)

Произведение равно нулю,когда хотя бы один из множителей равен нулю

1) 2sin²(x)-3cos(x) = 0

Из основного тригонометрического тождества sin²(x)+cos²(x) = 1 выразим синус

sin²(x) = 1-cos²(x)

2(1-cos²(x))-3cos(x) = 0

2-2cos²(x)-3cos(x) = 0|:(-1)

2cos²(x)+3cos(x)-2 = 0

Пусть cos(x) = t, -1 ≤ t ≤ 1, тогда

2t²+3t-2 = 0

D = 3²-4*2*(-2) = 9+16 = 25 = 5²

$\displaystyle t_{1} = \frac{ - 3 + 5}{2 \times 2} = \frac{2}{4} = \frac{1}{2}$

$\displaystyle t_{2} = \frac{ - 3 - 5}{2 \times 2} = - \frac{8}{4} = - 2$

Второй корень меньше -1,поэтому мы его рассматривать не будем

Вернёмся к замене

Если t = 0,5, тогда

cos(x) = 0,5

Это равенство распадается на совокупность двух:

[ x = arccos(0,5) + 2пn, n∈Z

[ x = -arccos(0,5) + 2пn, n∈Z

[ x = п/3 + 2пn, n∈Z

[ x = -п/3 + 2пn, n∈Z

Второй корень не подходит по ОДЗ,так что единственное решение этого равенства x = п/3 + 2пn, n∈Z

$\displaystyle \sqrt{ \tan(x) } = 0$

$\displaystyle { (\sqrt{ \tan(x) } ) }^{2} = {0}^{2}$

$\displaystyle \tan(x) = 0$

$\displaystyle \frac{ \sin(x) }{ \cos(x) } = 0$

Дробь равна нулю,когда числитель равен нулю,а знаменатель не равен нулю

{ sin(x) = 0

{ cos(x) ≠ 0

{ х = пn, n∈Z

{ x ≠ п/2 + пn, n∈Z

Пересечений с ОДЗ нет,поэтому наше решение входит в ответ

б) Находим количество решений на отрезке [0;2П] ( см. вложение)

По рисунку мы видим,что у уравнения на данном отрезке 4 корня(0,п/3,п,2п)

0,0(0 оценок)

Ответ:

sasoort1

21.04.2021 12:26

Задача. Сколько действительных корней имеет уравнение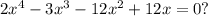 $2x^{4} - 3x^{3} - 12x^{2} + 12x = 0?$

Укажите интервал, которому принадлежит наименьший корень:

$1) ~ (-4; ~ {-}3);\\2) ~ (-3; ~ {-}2);\\3) ~ (-2; ~ {-}1);\\4) ~ (1; ~ 2);\\5) ~ (2; ~ 3).$

ответ запишите в виде: k, ~ m, где 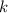— число корней, 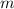— номер промежутка, которому принадлежит наименьший корень.

Решение. Вынесем общий множитель за скобки:

$x(2x^{3} - 3x^{2} - 12x + 12)=0.$

Произведение множителей равно нулю тогда, когда хотя бы один из них равен нулю:

1) ~ x = 0;

$2) ~ 2x^{3} - 3x^{2} - 12x + 12 = 0.$

Видя последнее уравнение, понимаем, что искать все его корни не нужно. Этого и не требуют в задании.

Рассмотрим функцию $f(x) = 2x^{3} - 3x^{2} - 12x + 12.$

1) Область определения: $D(f) = (-\infty; ~ {+}\infty).$

2) Исследуем данную функцию на четность:

$f(-x) = 2(-x)^{3} - 3(-x)^{2} - 12(-x) + 12 = -2x^{3} - 3x^{2} + 12x + 12 =\\= - (2x^{3} + 3x^{2} - 12x - 12) \neq -f(x).$

Функция не обладает свойством четности. Она ни четная, ни нечетная.

3) Определим нули функции.

3.1. Пересечение с осью $x \colon$

$2x^{3} - 3x^{2} - 12x + 12 = 0.$

Невозможно дать точный ответ.

3.2. Пересечение с осью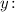 $y \colon$

$2 \cdot 0^{3} - 3\cdot 0^{2} - 12\cdot 0 + 12 = 12.$

Значит, (0; ~ 12) — точка пересечения с осью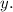

4) Найдем производную функции:

$f'(x) = 6x^{2} - 6x - 12.$

5) Определим критические точки функции, приравняв производную к нулю:

$6x^{2} - 6x - 12 = 0 ~~~ |: 6$

$x^{2} -x - 2 = 0$

$x_{1} = -1; ~ x_{2} = 2$

Определим точки экстремума и экстремумы функции:

$f' ~~~~~ + ~~~\max~~~~~ - ~~~~\min~~~+\\------|------|-----x\\f ~~~~~\nearrow~~~~ {-}1 ~~~~~~\searrow~~~~~~ 2~~~~~ \nearrow$

Итак:

$x_{\max} = -1; ~~~ x_{\min} = 2.$

$y_{\max} = 2 \cdot (-1)^{3} - 3 \cdot (-1)^{2} - 12 \cdot (-1) + 12 = 19$

$y_{\min} = 2 \cdot 2^{3} - 3 \cdot 2^{2} - 12 \cdot 2 + 12 = -8$

6) Изобразим схематически график функции, строго соблюдая все найденные точки, монотонность функции и симметрию линий около критических точек (см. вложение).

Выводы. Как видно из графика, из уравнения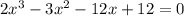 $2x^{3} - 3x^{2} - 12x + 12 = 0$ имеем три действительных корня, наименьший из которых находится в интервале 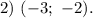2) ~ (-3; ~ {-}2). Таким образом, уравнение 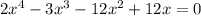$2x^{4} - 3x^{3} - 12x^{2} + 12x = 0$ имеет четыре действительных корня.