1) Преобразуйте выражение в многочлен стандартного вида и опре- делите его степень:
a) 3a? + 7b - 3a + 5ab + 2a+ + 3b2 - 6b - 3ab - 3b2 - 2ab; б) 3a(4a+3b)-9b(a-b)-12a2-8b2 +2ab.
2) Вынесите общий множитель за скобки:
a) 4b3 +8b2 -12b;
б) 12x'y -8x'y' +4x'y.
3) Решите уравнение
x-2 3x+1
3
4) Туристы некоторое расстояние со скоростью 4 км/ч и такое же расстояние проплыли на лодке со скоростью 6 км/ч. На весь этот путь было потрачено 5 часов. Какой путь преодолели туристы пешком и
на плоту?

если речь о натуральных числах

2012=2*2*503 -разложение в произведение простых чисел

чтобы наименьшее общее кратное семи чисел было равно 2012 в него должны входить числа кратные 503 и 4, наименьшие возможные (так как мы ищем наименьшую возможную сумму) будут 503 и 4, остальные чтоб быть наименее возможными должны равняться 1,

тогда сумма равна 1+1+1+1+1+4+503=512

если речь о целых числах то

2012=2*2*503 -разложение в произведение простых чисел

чтобы наименьшее общее кратное семи чисел было равно 2012 в него должны входить числа кратные 503 и 4, наименьшие возможные (так как мы ищем наименьшую возможную сумму) будут -503 и -4, остальные чтоб быть наименее возможными должны равняться -1,-1,-1,-1,1 (так чтоб произведение при этом равнолялось 2012)

тогда сумма равна -1+(-1)+(-1)+(-1)+1+(-4)+(-503)=-510

90 градусов.

Объяснение:

Пусть сторона квадрата равна . Тогда по условию, 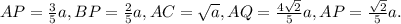Теперь попробуем найти стороны треугольника PQD:

1) найти PD:

По теореме Пифагора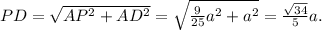

2) найти PQ и QD:

Проведем прямую проходящую через точку Q и параллельную BC, и отметим точки пересечения с квадратом ABCD как M и N где M∈AB, N∈CD и прямую проходящую через точку Q и параллельную AB, пересекающую квадрат в точках E и F где E∈BC, F∈AD.

Тогда из параллельности PQ||BC, FQ||CD и свойства пропорциональных отрезков получаем,

Следовательно из ,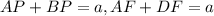

Также из-за того, что AP<AM,

Заметим что, AMQF - прямоугольник, тогда

Теперь нам известны катеты прямоугольных треугольников PMQ и QFD, значит мы можем найти и их гипотенузы PQ и QD,

3) доказать что ∠PQD=90°:

Действительно,

Из обратной теоремы Пифагора следует что, ∠PQD - прямой угол.

4) доказать что ∠PQD - наибольший угол соответствующего треугольника:

Предположим обратное, допустим в треугольнике PQD есть угол больший 90°, но тогда сумма углов этого треугольника будет больше 180° - противоречие.

По итогу имеем то что, ∠PQD=90° - наибольший угол треугольника PQD.