1). разложите на множители выражения: а). 12x+4x^2 б). 10a-5b-2ax+bx в).3•(4-x)^2-4•(x-4) 2). найдите значение выражения наиболее рациональным найдите все простые делители значения выражения 10^4-15^6. 4). найдите множество корней уравнения: а). 5x^4+x=0 б). (6-3x)^2=4x-8 в). 2x^2-10x^4+3x-15=0 5). разность двух натуральных чисел равна 1, а их произведение равно 72. найдите сумму этих чисел. 6). сравните меньший корень уравнения x^2-7x-6=0 с большим корнем уравнения x•|x|-x=0. 7). решите уравнение (a^2-4a)•x=a-3x-3 относительно переменной x в зависимости от параметра a. ! !

1. Решим квадратное уравнение: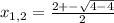 . Т. к. дискриминант равен нулю, то корень здесь один: 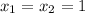. Парабола касается оси Ox в точке (1;0), а так как коэффициент при иксе в квадрате положительный, значит, ветви параболы направлены вверх. Из этого следует, что y>0 при x∈(-∞; 1)∪(1; +∞), а при x=1 функция равна нулю

2. Область определения функции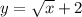 -- это x∈[0; +∞). Т. к. квадратный корень из числа всегда равен неотрицательному числу, к которому к тому же прибавляется два (в данной функции), то на всей области определения функция положительна: y>0 при x∈[0; +∞).

3. Область определения функции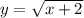 -- это x∈[-2; +∞). Функция равна нулю при x=-2, а на остальной области определения положительна: y>0 при x∈(-2; +∞).

Смотри. Вторая часть выражения - это результат вычисления в первой части выражения. Значит, чтобы понять, какие числа пропущены во второй части, мы должны закончить действия в первой. Действия будут следующие:

0,1k^2u^4 : 0,5ku^3 = 0,2ku - это первое пропущенное число после 8k^2 (вторая звёздочка).

12,5ku^5 : 0,5ku^3 = 25u^2 - это второе пропущенное число после 8k^2 (третья звёздочка)

А чтобы узнать первую пропущенную звёздочку, мы просто должны совершить обратное действие с числом 8k^2. А именно:

8k^2 * 0,5ku^3 = 4k^3u^3 - это и есть первая пропущенная звёздочка.

Надеюсь, понятно объяснил ;)