1.Решите неравенство и изобразите множество решений на координатной прямой:
25-х>2-3(х-6)
2х-4(х-8)≤3х+2
2.При каких значениях y значение выражения 15 + y меньше значений выражения
16-y?
3.Решите систему неравенств:
1) 6-3х>0, 2)3х-2≥х+1,
5х-3>0. 4-2х≤х

Максимум в точке х =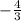 (для записи )

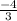Минимум в точке х = -1

Объяснение:

f(x)=2x^3+7x^2+8x+4

Область определения:

Х∈R

f(x)=2x^3+7x^2+8x+4, Х∈R

Определим производную f:

f(x) = 2x^3+7x^2+8x+4

f'(x) = d/dx (2x^3+7x^2+8x+4)

f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)

f'(x) = 2*3x^2 + 7*2x+8+0  

f'(x) = 6x^2+14x+8

f'(x) = 6x^2+14x+8, Х∈R

Представим f'(x) = 0

0=6x^2+14x+8

Решим ур-е относительно Х

6x^2+14x+8=0 | :2

3x^2+7x+4=0

D=b2-4ac = 7^2-4*3*4 = 1

x1,2= -b+-D/2a = -7+-1/2*3

x1= - 4/3

х2= -1

X∈(-∞;- 4/3)

X∈(- 4/3;-1)

max: - 4/3

min: -1

1) Показательная функция с основанием 6>1 монотонно возрастает. Большему значению функции соответствует большее значение аргумента:
х²+2х>3      или    х²+2х-3>0           или    (х+3)(х-1)>0
---------------(-3)--------------(1)----------------------
\\\\\\\\\\\\\\\\\\\\\                        ////////////////////
ответ. (-∞;-3)U(1;+∞)
2)
   Показательная функция с основанием 7>1 монотонно возрастает. Поэтому каждое свое значение  только в одной точке. Если значения функции равны, то и аргументы равны:
 x-2=1/2    ⇒x=2,5
ответ. 2,5
3) 25=5²
Показательная функция с основанием 7>1 монотонно возрастает. Поэтому каждое свое значение  только в одной точке. Если значения функции равны, то и аргументы равны:
х²-2х-1=2
х²-2х-3=0
(х+1)(х-2)=0
х=-1    или    х=2
ответ. -1; 2
4) Замена переменной 
t²-5t+4=0
D=25-16=9
t=1    или   t=4
  ⇒   x=0
  ⇒   x=2
ответ. 0; 2
5)Замена переменной 
t²-6t+5=0
D=36-20=16
t=1      или   t=5
  ⇒   x=0
  ⇒   x=1
ответ. 0; 1