1)Сколько шестизначных чисел делится на 5? А) 18*10⁴ В) 9*10⁴ С) 5*6! Д) 6*5⁴ 2) Сколько пятизначных чисел можно составить из цифр 1,2,3,4,5,6,7,8, если они могут повторяться? Можно ответ с решением
Конечно можно занятся исследованием функций, находить производные, но тут максимально упрощена задача.
1) просто построй функцию на отрезке [-2;1] подставив точки -2, -1, 0, 1. Этого будет достаточно, чтобы увидеть, что наименьшее значение будет в точке (0;0) равное 0, а наибольшее в точке (-2;64) равное 64. Так как графиком будет являтся суженная парабола.
2) то же самое. Чтобы узнать сколько корней, надо построить график левой части и правой части, и посмотреть есть ли у графиков точки пересечения. Сколько точек пересечения столько и корней.
построй график на отрезке [-2;2]. Этого будет достаточно. График снова суженная парабола.
и график на том же отрезке, а здесь будет прямая, которая уйдет вниз, и у нее не будет общих точек пересечения с параболой.
В итоге,существует расставить 2 ученикам 2 оценки (4 и 5).
А если прибавить к ним еще одного ученика - С. То:
А Б С 4 4 4 5 5 5 4 4 5 4 5 5 5 5 4 5 4 4 4 5 4 5 4 5
В итоге получаем
А что если, оставим тех же 2 учеников, но добавим 1 оценку - 3?
А вот что получим:
А Б 3 3 4 4 5 5 3 4 4 3 4 5 5 4 3 5 5 3
В итоге, мы получили
Нет смысла, добавлять 3 ученика. Уже и так можно увидеть закономерность.
В 1 раз, мы имели 2 ученика и 2 оценки, отметим это как: В 2 раз, мы имели 3 ученика и 2 оценки, отметим это как: В 3 раз, мы имели 2 ученика и 3 оценки, отметим это как:
А теперь, выведем формулу: - где a-число оценок, b-число учеников.
В итоге и получаем: 1 случай: 2 случай: 3 случай:
Теперь, вычислим наш случай в задаче. Есть 24 ученика = b, и 4 оценки=a (2,3,4,5). Отсюда:
Второй
Для первого ученика существует 4 варианта: 2,3,4,5 Для второго ученика существует 4 варианта на каждый вариант первого ученика. То есть: - варианта событий.
Для третьего ученика существует 4 варианта на каждый вариант второго ученика. То есть: - варианта событий.
И так далее. В итоге получаем, что для 24 учеников существует ровно:
Конечно можно занятся исследованием функций, находить производные, но тут максимально упрощена задача.
1) просто построй функцию на отрезке [-2;1] подставив точки -2, -1, 0, 1. Этого будет достаточно, чтобы увидеть, что наименьшее значение будет в точке (0;0) равное 0, а наибольшее в точке (-2;64) равное 64. Так как графиком будет являтся суженная парабола.
2) то же самое. Чтобы узнать сколько корней, надо построить график левой части и правой части, и посмотреть есть ли у графиков точки пересечения. Сколько точек пересечения столько и корней.
построй график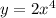
на отрезке [-2;2]. Этого будет достаточно. График снова суженная парабола.
и график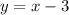
на том же отрезке, а здесь будет прямая, которая уйдет вниз, и у нее не будет общих точек пересечения с параболой.
Значит корней здесь нет.
1 ученик - А
2 ученик - Б
Получаем:
А Б
4 5
5 4
5 5
4 4
В итоге,существует расставить 2 ученикам 2 оценки (4 и 5).
А если прибавить к ним еще одного ученика - С. То:
А Б С
4 4 4
5 5 5
4 4 5
4 5 5
5 5 4
5 4 4
4 5 4
5 4 5
В итоге получаем
А что если, оставим тех же 2 учеников, но добавим 1 оценку - 3?
А вот что получим:
А Б
3 3
4 4
5 5
3 4
4 3
4 5
5 4
3 5
5 3
В итоге, мы получили
Нет смысла, добавлять 3 ученика. Уже и так можно увидеть закономерность.
В 1 раз, мы имели 2 ученика и 2 оценки, отметим это как:
В 2 раз, мы имели 3 ученика и 2 оценки, отметим это как:
В 3 раз, мы имели 2 ученика и 3 оценки, отметим это как:
А теперь, выведем формулу:
В итоге и получаем:
1 случай:
2 случай:
3 случай:
Теперь, вычислим наш случай в задаче. Есть 24 ученика = b, и 4 оценки=a (2,3,4,5).
Отсюда:
Второй
Для первого ученика существует 4 варианта:
2,3,4,5
Для второго ученика существует 4 варианта на каждый вариант первого ученика.
То есть:
Для третьего ученика существует 4 варианта на каждый вариант второго ученика.
То есть:
И так далее. В итоге получаем, что для 24 учеников существует ровно: