1. Вставить между числами -4 и 5 пять таких чисел, которые вместе с данными составляли бы арифметическую прогрессию.
2. Найдите наибольший отрицательный член арифметической прогрессии 2; 1,8; 1,6; ... .
3. Найти сумму шестнадцати первых членов арифметической прогрессии (Аn), если А1 = 3, А16 = -5;
4. Найти сумму шестнадцати первых членов арифметической прогрессии (Аn), если А1 = 6, d = 3;

Показать ответ

Ответ:

tanyalepihina2

05.05.2023 10:27

просто подряд подставлять целые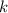

при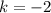 k=-2 имеем корни

$x_1=-\frac{\pi}{3}-4\pi=\frac{-13\pi}{3},\\x_2=\frac{4\pi}{3}-4\pi=-\frac{8\pi}{3},\\x_3=\frac{\pi}{2}-2\pi=-\frac{3\pi}{2}$

Первые два в промежуток не попадают, третий - попадает.

при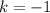 k=-1 имеем корни

$x_1=-\frac{\pi}{3}-2\pi=-\frac{7\pi}{3},\\x_2=\frac{4\pi}{3}-2\pi=-\frac{2\pi}{3}\\x_3=\frac{\pi}{2}-\pi=-\frac{\pi}{2}$ ,

первый корень в промежуток не попадает, другие два - попадают.

Если подставлять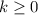 $k\geq 0$ , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.

универсальный, но не очень удобный): оценить и проверить, при каких целых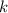 неравенство 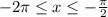$-2\pi\leq x\leq -\frac{\pi}{2}$ имеет решение. Для этого все серии корней по отдельности подставляем вместо :

$1) -2\pi\leq -\frac{\pi}{3}+2\pi k\leq -\frac{\pi}{2} |\cdot\frac{3}{\pi} ,\\-6\leq -1+6k \leq -\frac{3}{2}|+1\\-5\leq 6k\leq -\frac{1}{2} |:6\\-\frac{5}{6}\leq k\leq -\frac{1}{12}.$

Очевидно, что целых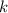 , удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.

$2) -2\pi\leq \frac{4\pi}{3}+2\pi k \leq -\frac{\pi}{2}|\cdot\frac{3}{4\pi}\\ -\frac{3}{2} \leq 1+\frac{3}{2}k\leq -\frac{3}{8}|-1\\-\frac{5}{2}\leq \frac{3}{2}k\leq -\frac{11}{8}|\cdot\frac{2}{3}\\-\frac{5}{3}\leq k\leq -\frac{11}{12}$

Последнему неравенству удовлетворяет только одно целое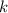 - 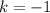k=-1 . Корень находим при подстановке значения 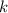в соответствующую серию.

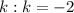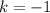То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения k: k=-2 и k=-1 . Их также подставляем в соответствующую серию и находим корни.

0,0(0 оценок)

Ответ:

LeylaAllesgerova

31.05.2022 17:55

Высказывание "Если А, то В" (импликация) ложно тогда и только тогда, когда А истинно, а В - ложно.
Если говорящий рыцарь, то произнесённое им высказывание истинно.
Высказывание "Я рыцарь" - истинно.
Высказывание "истина -- > А" истинно тогда и только тогда, когда А истинно.
"Съем собственную шляпу" - истинно, придётся съесть.
Если говорящий лжец, то высказывание "Я рыцарь" - ложно.
Высказывание "ложь -- > А" всегда истинно, независимо от того, какое А.
"Если я рыцарь, то съем собственную шляпу" - истинно, что для лжеца невозможно.
Итак, говорящий - рыцарь и ему придётся съесть шляпу.

0,0(0 оценок)

Популярные вопросы: Алгебра