1 .Выберите уравнение, с которого задана линейная функция

у= х² + 8х
у= х³
у = 2х+8
у= 8/х

2.Если k= - 9 и b = - 9, то линейная функция имеет вид

у = - 9х - 9
у = -9х + 9
у= - 9х
у = -9

3.Выберите функцию график, которой расположен в I и III координатных четвертях

у = - х + 9
у= -3 -7х
у = 2х
у= - 4,5

4.Найдите значение функции у = 2х -12 в точке, абсцисса которой равна 4

4
-10
- 4
20

5.Какой из указанных прямых принадлежит точка А (-3; 8)

у= - 3х+ 8
у= 2х+14
у = 8
у= -3х

6.Определите угловой коэффициент функции, заданной уравнением у = 1,2 - 7х

1,2
-1,2
7
- 7

7.Определите точку, которая принадлежит графику функции, заданной уравнением у= 5 - 2х

С(-5;5)
В(5;-5)
А(-5;-5)
Д(5;5)

8.Укажите ложное утверждение

график функции у = 7 расположен в I и II координатных четвертях
график функции х = 3 параллелен оси ординат
графики функций у = 2х и х = 4 пересекаются
графики функций х = 3 и х = - 4 взаимно перпендикулярны

9.Для функции у = 1/4 х + 1,5 укажите ложные утверждения

это - линейная функция
график функции параллелен оси абсцисс
b=1,5; к=1/4
точка А(0;1,5) принадлежит графику функции

10.Выберите точку, в которой график функции у= - 0,75х - 5 пересекает ось ординат

А(0; -5)
С(-5;0)
Д(0;0)
В(1;-5,75)

Показать ответ

Ответ:

Косалинааа

18.02.2020 11:53

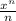Ну $\frac{x^n}{n}$ указывает на то, что надо бы производную брать для исследования этой функции, ибо она красивая получается.

f'(x)=x^4-x^3+x^2+x-2;

Далее, для исследования исходной функции на возрастание/убывание необходимо найти нули производной, то есть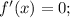 f'(x)=0;

x^4-x^3+x^2+x-2=0;

Сумма коэффициентов в уравнении равно 0, значит, x=1 - корень

Попробуем разложить выражение, заранее зная корень.

$x^4-x^3+x^2+x-2=x^4-x^3+x^2-x+2x-2=\\ =x^3(x-1)+x(x-1)+2(x-1)=(x-1)(x^3+x+2)$

Теперь нужно проанализировать правую скобку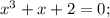 x^3+x+2=0;

Сумма коэффициентов при четных (2) и нечетных (1+1=2) степенях равна, значит, x=-1 - корень.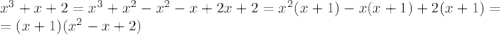 $x^3+x+2=x^3+x^2-x^2-x+2x+2=x^2(x+1)-x(x+1)+2(x+1)=\\ =(x+1)(x^2-x+2)$

Осталась последняя скобка в разложении, найдем дискриминант уравнения

x^2-x+2=0; D=(-1)^2-4*1*2=1-8=-70 при любых х.

Итоговое разложение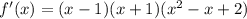 f'(x)=(x-1)(x+1)(x^2-x+2)

Нули производной известны, это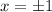 $x=\pm1$

Везде при х коэффициент равен 1 (у правой скобки нет нулей, её мы считаем просто каким-то положительным числом), значит, в самом правом промежутке "+", а дальше чередование.

Имеем при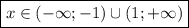 $\boxed {x \in (-\infty;-1)\cup(1;+\infty)}$ возрастание 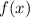f(x) , а при 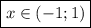$\boxed {x\in(-1;1)}$ убывание f(x) ,

x=-1 - точка локального максимума,

x=1 - точка локального минимума.

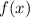Убывание должно быть на интервале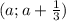 $(a; a+\frac{1}{3})$ , поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.

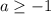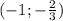С одной стороны, $a\geq -1$ , как раз при a=-1 убывание на $(-1;-\frac{2}{3})$ выполняется.

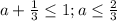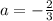С другой стороны, $a+\frac{1}{3}\leq 1; a\leq \frac{2}{3}$ , при $a=-\frac{2}{3}$ убывание продолжается вплоть до x=1, не включая эту точку.

Объединяя наши условия, получаем $$1\leq a\leq \frac{2}{3} \Rightarrow a\in[1;\frac{2}{3}]$

ответ: $\boxed {a\in[1;\frac{2}{3}]}$

0,0(0 оценок)

Ответ:

КАТЯЯЯЯЯ111

29.03.2020 21:51

1. 25 - 36p²c² = 5²-(6рс)² = (5-6рс)(5+6рс)
(3+y)² - 4 = (3+у)²-2² = (3+у-2)(3+у+2) = (у+1)(у+5)
(3x+1)² - (4x-3)² = (3х+1-4х+3)(3х+1+4х-3) = (-х+4)(7х-2)
100 - 49x²y² = 10²-(7ху)² = (10-7ху)(10+7ху)
(5+x)² - 9 = (5+х)²-3² = (5+х-3)(5+х+3) = (х+2)(х+8)
(2a + 7)² - (3a - 5)² = (2а+7-3а+5)(2а+7+3а-5) = (-а+12)(5а+2)

2. x²ⁿ - 9 = (хⁿ)²-3² = (хⁿ-3)(хⁿ+3)
b² - a⁴ⁿ = b² - (a²ⁿ)² = (b-a²ⁿ)(b+a²ⁿ)
x²ⁿ - y²ⁿ = (хⁿ)²-(уⁿ)² = (хⁿ-уⁿ)(хⁿ+уⁿ)
81a⁸ⁿ - 16 = (9а⁴ⁿ)²-4² = (9а⁴ⁿ-4)(9а⁴ⁿ+4) = (3а²ⁿ-2)(3а²ⁿ+2)(9а⁴ⁿ+4)
a²ⁿ - 1 = (аⁿ)²-1² = (аⁿ-1)(аⁿ+1)
x²- y⁴ⁿ = х²-(у²ⁿ)² = (х-у²ⁿ)(х+у²ⁿ)
a⁴ⁿ - b⁴ⁿ = (а²ⁿ)²-(b²ⁿ)² = (a²ⁿ-b²ⁿ)(a²ⁿ+b²ⁿ) = (aⁿ-bⁿ)(aⁿ-bⁿ)(a²ⁿ+b²ⁿ)
49x^6m - 25 = (7x^3m)² - 5² = (7x^3m - 5)(7x^3m + 5)

0,0(0 оценок)

Популярные вопросы: Алгебра