1.Вычислите значение выражения 4^(1/2)+8^(2/3)+√(16.)
2.Найдите значение cos a , если известно, что sin a= 1/2 и 0 < a <( π)/( 2)
3.Решите уравнение 2^(4х+1)=16^2х.
4.Решите уравнение 1/3 √(х-5)=4
5.Решите уравнение соs^2 х+sinx=-sin^2 x
6.Основанием прямой призмы является ромб со стороной 14 см и углом 30 °. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: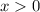 ).
).
Пусть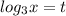 , тогда:
, тогда:
Тогда:
1).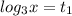
(таким числом под логарифмом будет 27: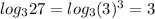 )
)
2).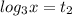
(таким числом под логарифмом будет 3: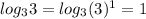 )
)
ответ: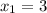 ,
, 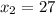
формулой.
Функции подразделяются на следующие виды:
Линейная функция
Квадратичная функция
Кубическая функция
Тригонометрическая функция
Степенная функция
Показательная функция
Логарифмическая функция
Область определения функции D(у) - это множество всех допустимых значений аргумента x (независимой переменной x), при которых выражение, стоящее в правой части уравнения функции y = f(x) имеет смысл. Другими словами, это область допустимых значений выражения f(x).
Чтобы по графику функции y = f(x) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
Множество значений фнкции Е(у) - это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции y = f(x) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
Обратная функция — функция y=g(x), которая получается из данной функции y = f(x), если из отношения x = f(у) выразить y через x.
Чтобы для данной функции y = f(x) найти обратную, надо:
В соотношении y = f(x) заменить x на y, а y — на x: x = f(у) .
В полученном выражении x=f(у) выразить y через x.
Функции f(x) и g(x) — взаимно обратны. Рассмотрим это на примере
Примеры нахождения обратных функций:
size 12px 1 size 12px right parenthesis size 12px space size 12px space size 12px y size 12px equals size 12px 3 size 12px x size 12px minus size 12px 8
size 12px space size 12px space size 12px space size 12px space size 12px space size 12px space size 12px x size 12px equals size 12px 3 size 12px y size 12px minus size 12px 8 size 12px rightwards double arrow size 12px 3 size 12px y size 12px equals size 12px x size 12px plus size 12px 8 size 12px rightwards double arrow fraction numerator size 12px x size 12px plus size 12px 8 over denominator size 12px 3 end fraction
size 12px 2 size 12px right parenthesis size 12px space size 12px space size 12px y size 12px equals size 12px 11 size 12px minus size 12px 5 size 12px x
size 12px space size 12px space size 12px space size 12px space size 12px space size 12px space size 12px x size 12px equals size 12px 11 size 12px minus size 12px 5 size 12px y size 12px rightwards double arrow size 12px 5 size 12px y size 12px equals size 12px 11 size 12px minus size 12px x size 12px rightwards double arrow size 12px y size 12px equals fraction numerator size 12px 11 size 12px minus size 12px x over denominator size 12px 5 end fraction