1.яку цифру між цифрами 16 щоб утворене в такий б число ділилось на 9?

Показать ответ

Ответ:

Даша5015664

02.10.2022 19:18

пусть цифры числа будут A и B

тогда

A^3+B^3 = 91

(A+B)AB=84

(a + b)(a^2 - ab + b^2)=91

(A+B)AB=84

рассмотрим первое уравнение: так как а и в цифры числа - то они являются натуральными числами. отсюда следует что а+в и a^2-ab+b^2 натуральные числа.

число 91 разложить на множители можно 2-мя это 1*91 и 7*13

первый вариант неподходит (если а+в=1 то а либо б = 0 тогда значение a^2-ab+b^2 будет равно 1 если а+в=91 то a^2 - ab + b^2 небудет равно 1 так как разность суммы квадратов чисел и произведения этих чисел будет больше 1)

второй вариант:

2.1

a + b = 7

a^2 - ab + b^2 = 13

выразим а а=7-в

(7-b)^2-b(7-b)+b^2-13=0

49-14b+b^2-7b+b^2+b^2-13=0

3b^2-21b=-36

3b^2-21b+36=0

b^2-7b+12=0

d=1

b1=3 b2=4 a1=4 a2=3

2.2

a + b = 13

a^2 - ab + b^2 = 7

а=13-b

(13-b)^2 -b(13-b)+b^2=7

169-26b+b^2-13b+b^2=7

169-39b+3b^2=7

3b^2-39b+162=0

b^2-13b+54=0

d=169-216

уравнение решений не имеет.

тогда получаем два возможных а и б (4 и 3) (3 и 4)

подставим значения а и б в уравнение (A+B)AB=84 оба значения а и б удовлетворяют уравнению.

ответ: такие числа 43 и 34

0,0(0 оценок)

Ответ:

паксуха

14.09.2021 10:46

$\left \{ {{x^2-xy+y^2=7} \atop {x^2+2xy+2y^2=5}} \right$

Сложим первое уравнение,домноженное на 2 со вторым:

3x^2+4y^2=19

Очевидно,что x и y не обращаются в ноль,так как число 19 простое и не имеет делителей на интервале (1;19)

Значит:

$\left \{ {{3x^2=19-4y^2<19} \atop {4y^2=19-3x^2<19}} \right$

$\left \{ {{x^2=<6\frac{1}{3}} \atop {y^2<4\frac{3}{4}}} \right$

$\left \{ {{|x| \in [1;2]} \atop {|y| \in [1;2]}} \right$

Из полученных отрезков лишь пара значений модулей удовлетворяет нашему уравнению:

(|x|;|y|)=(1;2)

Осталось лишь раскрыть модуль,сделаем это следующим образом:

Рассмотрим полиномы вида:

$\left \{ {{F_1(x,y)=x^2-xy+y^2-7} \atop {F_2(x,y)=x^2+2xy+2y^2-5}} \right$

Подставим модули корней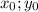 x_0;y_0 под степени 2,так как они являются четными и не меняют значение:

$\left \{ {{F_1(x_0,y_0)=|1|^2-x_0y_0+|2|^2-7} \atop {F_2(x_0,y_0)=|1|^2+2x_0y_0+2|2|^2-5}} \right$

$\left \{ {{F_1(x_0,y_0)=-x_0y_0-2} \atop {F_2(x_0,y_0)=2x_0y_0+3}} \right$

Очевидно,что для старших мономов вида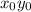 x_0y_0 обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.