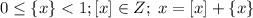1. Зведіть подібні члени многочлена: а 3
– 4 + 6а2 + а – 3а3 + 5а.
2. Подайте у вигляді многочлена стандартного вигляду вираз:
1) (3х + 9) + (–х
2
– 15х – 40);
2) (13ху – 11х
2
+ 10у
2
) – (–15х
2
+ 10ху – 15у
2
).
3. Виконайте множення:
1) 2х (3х
2
– 4х + 5);
2) (х – 3)(х + 2);
3) (7а – b)(5b + 6a);
4) (2x – y)(4x
2
+ 2xy + y
2
).
4. Розкладіть на множники:
1) 4а
2
+ 16аb;
2) 15c
6
– 3c
4
;
3) 5a – 5b + ap – bp;
4) a (c – d) + b (d – c);
5) х
5
+ х
3
– х
2
– 1;
6) az
2
– bz2
– bz + az – a + b.
5. Розв’яжіть рівняння (3x – 5)(2x + 7) = (3x + 1)(2x – 3) + 4x.
6. Спростити вираз:
1) 6а (2а – 3) – (а –1)(а + 4).
2) (x + 5)(x
2
– 2x – 3) – (5x + x
2
)(x – 2) + 3(x + 5).
7. Розв’яжіть рівняння:
1)

;
2) 15у – 5у
2
= 0.
8. Розкладіть на множники та обчисліть значення виразу
х
2
– 4ху + 2ху – 8у
2
, якщо х = 1,5, у = 0,25.

Показать ответ

Ответ:

gvozd1

22.06.2021 19:48

Трололо, с русским тоже бяда.

1) 800 * 5% = 800 * 0.05 = 40 - скидка
800 - 40 = 760 - цена чайника
1000 - 760 = 240 - сдача.

2) √35 чуть меньше чем 6. Подумай, почему.
√120 - почти 11.
В порядке возрастания (если нужно будет в обратном, поменяешь местами): 2, 3, √35, 6.5, √120, 13.

3) Трапеция прямоугольная, значит одна боковая сторона тоже образует прямые углы с основаниями, как у квадрата. Эта сторона будет меньше, так как расположена под прямым углом, следовательно равна 9. Большая - 15. Отсекаем прямоугольник, проводя высоту с другой стороны трапеции, остаётся треугольник со сторонами 9, 15 и одной неизвестной, которую находим по теореме Пифагора:
15^2 = x^2 + 9^2
15^2 - 9^2 = x^2
x^2 = 225 - 81 = 144;
x = √144

Большее основание = меньшее основание + X.

0,0(0 оценок)

Ответ:

taniussa1

16.04.2023 07:24

По определению,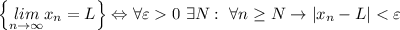 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение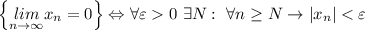 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

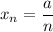
2) $x_n=\dfrac{a}{n}$

|x_n|

А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1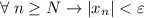$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: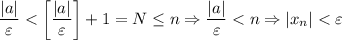 $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

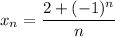
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1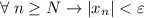$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда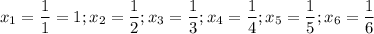 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$