178. Знайди значення виразів зі змінною. Запиши
80 374-х. 234, якщо x=73.
Відповідь:
14943+с. 367, якщо с= 42.
Відповідь:

Показать ответ

Ответ:

Kristinapermya

29.05.2021 19:24

Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2

найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).

Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим

$(ax+1)^2+x(ax+1)-4x-9(ax+1)+20=0\\ a^2x^2+2ax+1+ax^2+x-4x-9ax-9+20=0\\ x^2(a^2+1)-(3+7a)x+12=0$

Найдем дискриминант квадратного уравнения относительно x

$D=(3+7a)^2-4(a^2+1)\cdot12=9+42a+49a^2-48a^2-48=\\ =a^2+42a-39=0$

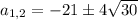
Получим $a_{1,2}=-21\pm4\sqrt{30}$

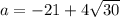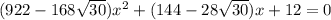Если подставить $a=-21+4\sqrt{30}$ , т.е. имеется квадратное уравнение $(922-168\sqrt{30})x^2+(144-28\sqrt{30})x+12=0$ , у которого корень

$\bigg(x-\dfrac{36+7\sqrt{30}}{29}\bigg)^2=0\\ \\ x=\dfrac{36+7\sqrt{30}}{29}2$

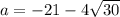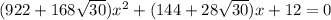Если подставить $a=-21-4\sqrt{30}$ , т.е. имеется квадратное уравнение $(922+168\sqrt{30})x^2+(144+28\sqrt{30})x+12=0$ , у которого корень

$\bigg(x-\dfrac{36-7\sqrt{30}}{29}\bigg)^2=0\\ \\ x=\dfrac{36-7\sqrt{30}}{29}$

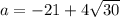
ответ: $a=-21+4\sqrt{30}$

0,0(0 оценок)

Ответ:

azerzhanovaa

08.08.2021 04:54

Запишем, какие числа удовлетворяют условию задачи:
11, 13, 15, ..., 99 - двузначные натуральные нечетные
Найдем их общее количество: последовательность является арифметической прогрессией, где:

чисел
а)

Нечетное число:
Числа, удовлетворяющие условию: 11, 13, ..., 31
Их количество:

Вероятность:
б)

Условию будут удовлетворять числа: 91, 93, 95, 97, 99 (5 шт.)
Вероятность:
в)
Если х=9, то у=9
Если х=8, то у=9
Получаем числа: 99, 89 (2 шт.)
Вероятность:
г)
Если х=1, то у=1; 3
Если х=2, то у=1
Если х=3, то у=1
Числа: 11, 13, 21, 31 (4 шт.)
Вероятность:

0,0(0 оценок)

Популярные вопросы: Алгебра