Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
Объяснение:
Периметр - сумма длин всех сторон:
Р=(-1-2b)+(-2b-)+(3a+6ab).
Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
В нашем случае нужно раскрыть скобки и привести подобные слагаемые:
-1-2b+-2b-+3a+6ab - подобных слагаемых нет. Располагаем все эти слагаемые в порядке понижения степени:
2b-+6ab+3a-2b-1.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов; в нашем случае - наибольшая степень - это 2.
Как это теперь записать:
Р=(-1-2b)+(-2b-)+(3a+6ab)=-1-2b+-2b-+3a+6ab=2b-+6ab+3a-2b-1; степень многочлена - 2.
Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
Объяснение:
Периметр - сумма длин всех сторон:
Р=(-1-2b)+(-2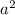 b-
b-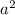 )+(3a+6ab).
)+(3a+6ab).
Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
В нашем случае нужно раскрыть скобки и привести подобные слагаемые:
-1-2b+-2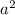 b-
b-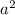 +3a+6ab - подобных слагаемых нет. Располагаем все эти слагаемые в порядке понижения степени:
+3a+6ab - подобных слагаемых нет. Располагаем все эти слагаемые в порядке понижения степени:
2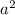 b-
b-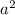 +6ab+3a-2b-1.
+6ab+3a-2b-1.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов; в нашем случае - наибольшая степень - это 2.
Как это теперь записать:
Р=(-1-2b)+(-2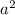 b-
b-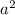 )+(3a+6ab)=-1-2b+-2
)+(3a+6ab)=-1-2b+-2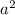 b-
b-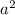 +3a+6ab=2
+3a+6ab=2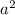 b-
b-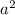 +6ab+3a-2b-1; степень многочлена - 2.
+6ab+3a-2b-1; степень многочлена - 2.