2. разложить на множители:
а) y² — 36;
в) 16m^6n² — 81х²;
б) n² — 10n + 25; г) (x + 2)² – (х – 2)².
3. выражение:
(y+4)² – 5y(у — 6).
4. решите уравнение:
а) х(х – 4) + (3 – x)(3 +х) = – 6;
б) 81y²– 100 = 0.
5. выполнить действия:
а) (9c² +d²) (3c — d)(3c + d);
б) (5х⁴ — 7y²)(5х⁴ + 7y²).
6. докажите неравенство: 81x² +4y² > 36xy -8.​

25

Объяснение:

решения.

Выпишем несколько первых натуральных чисел кратных 5:

5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).

Пронумеруем члены последовательности:

Число, следующее за четвертым членом последовательности 25.

решения.

Воспользуемся формулой для нахождения n-го члена арифметической последовательности.

Наименьшее натуральное число делящееся на 5 это 5, т.е. .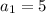

Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е. .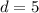

Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.

Рабочие производили детали 17 дней и произвели 1156 деталей.

Объяснение:

Допустим x - максимальное количество дней. Тогда x-2 - это количество затраченных дней.

(x-2)*68 = 60x - если производить 68 деталей в день x-2 дней, то получится то же кол-во, если производить 60 деталей x дней.

Решаем уравнение

68x-136 = 60x

68x - 60x = 136

8x = 136

x = 136/8

x = 17

ответ: на изготовление деталей ушло 17 дней.

Рабочие 17 дней производили 68 деталей в день. Значит кол-во деталей равно 17*68

17*68 = 1156

ответ: 1156 деталей произвели рабочие.

Если есть вопросы, пиши