2В) Вычислите: 204. 1А) Запишите в порядке возрастания 0,5/11, 2,5 , 2/0,7.
2 -
2
2 + 3
3 3 — 1
3B) Найдите площадь прямоугольника, если известно, что сум-
ма длин двух его смежных сторон равна /14 см, а их разность
10 см.
4B) Докажите, что при всех допустимых положительных значе-
ſa b-b
(а - b)?
ниях а и b верно равенство
ſa b + b
+b a² - b b
5C) Постройте график функции y =-x +4 и найдите, при каких
Значениях х;
1) у = 0; 2) у > 0; 3) у < 0.​

Нам нужно составить линейную систему уравнений вида

Вместо коэффициентов a,b,c,d подставляем какие-то числа, которые нам в голову придут, чтобы вычислить e и f подставим ещё x,y из задания

a)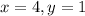

Пусть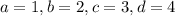

Получаем систему

Решим её

Решение действительно как в задании, значит, все верно сделано.

Аналогично со второй системой

б) пусть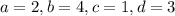

Система:

Решение совпадает с тем, что указано в задании, все верно.

P.S. по поводу придумывания коэффициентов.

1. Они не должны быть все нулевые

2. Любое из двух уравнений системы не должно выводиться из другого уравнения системы. Пример:

Видно, что второе уравнение - первое уравнение, умноженное на 2. Такого тоже не должно быть. Вообще такие уравнения являются линейно зависимыми.

То есть не все числа подойдут, небольшое ограничение есть)

912.

Сначало всё обозначим:

скорость лодки х ;

скорость лодки против чтения х-4 ;

время пути по реке 20/х-4 ;

время пути по озеру 14/х.

Разница между тем и другим временем 1 час по условию. Составляем уравнение:

20/х-4 - 14/х = 1

Приводим к общему знаменателю, перемножаем, получаем квадратное уравнение:

х^2 - 10х - 56 = 0

По формуле квадратных корней находим

х1 = - 4

отбрасываем, отрицательной скорости не бывает,

х2 = 14

принимаем, это собственная скорость лодки. Скорость лодки против течения 14 - 4 = 10 (км/ч)

914.

(знаки это дробь)

Так как скорость не может принимать отрицательное значение, следовательно искомый ответ : 40.

ответ : Токарь должен был обрабатывать 40 деталей в час по плану.

915.

Решение.

Пусть х изделий бригада должна была изготовить в 1 день по плану

(120/х) дней - бригада должна работать

(х+2) - изделия

Бригада изготовляла фактически в 1 день 120/(х+2) дней - бригада работала фактически.

А так как, по условию задачи, бригада закончила работу на 3 дня раньше срока, то составим уравнение:

120/х - 120/(х+2) = 3

120(х+2) - 120х = 3х(х+2)

120х+240 - 120х - 3х² - 6х = 0

3х² + 6х - 240 = 0

х² + 2х - 80 = 0

D = 4 + 4 × 1 × 80 = 324

x¹ = (-2 - 18)/2 = - 10 < 0 не удовлетворяет условию задачи

х² = (-2 + 18)/2 = 8

8 - изделий бригада рабочих изготовляла в 1 день по плану.

ответ : 8 изделий.

Нуу вроде всё)