Алгебра: 2вариант подскажите буду

2вариант подскажите
буду

Показать ответ

Ответ:

ulozerova

28.06.2022 18:59

ОТВЕТ: 1/15.

Решение Пусть событие А - оба шара черные.

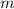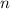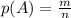Воспользуемся классическим определением вероятности. Вероятность события А найдем как отношение числа благоприятных исходов к числу всех возможных исходов: $p(A)=\frac{m}{n}$ .

Всего шаров 7 + 3 = 10. Выбрать 2 шара из 10 - поскольку не учитывается порядок - можно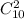 $C_{10}^{2}$ поэтому

$n=C_{10}^{2}=\frac{10!}{2!(10-2)!}=\frac{10\cdot9}{2}=45.$

Выбрать 2 черных шара из 3 можно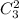 C_3^2 поэтому

$m=C_3^2=\frac{3!}{2!(3-2)!} =\frac{3}{1}=3.$

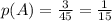
Итого $p(A)=\frac{3}{45}=\frac{1}{15}$

Разобьем событие как бы на два других: В - первый шар будет черным; С - второй шар будет черным.

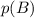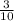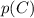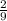Вероятность p(B) того, что первый шар будет черным, по определению вероятности равна $\frac{3}{10}$ , поскольку всего шаров 10, а черных - 3. После того, как взяли один черный шар, всего осталось 9 шаров, из которых 2 черных. Поэтому вероятность p(C) того, что второй шар будет черный, равна $\frac{2}{9}$ .

Поскольку необходимо, чтобы одновременно и первый, и второй шар были черными, искомую вероятность можно найти, перемножив вероятности событий В и С, т.е.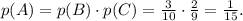 $p(A) = p(B)\cdot p(C)=\frac{3}{10}\cdot\frac{2}{9}=\frac{1}{15}.$

0,0(0 оценок)

Ответ:

helena59

07.02.2021 17:47

Всего 10 цифр : 0,1,2,3,4,5,6,7,8,9

Трёхзначное число содержит три цифры, по условию только одна из которых 3.

1) Числа вида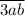 $\overline{3ab}$ . Цифры a и b могут быть любыми из оставшихся девяти цифр. Всего трёхзначных чисел с единственной тройкой в разряде сотен 9·9=81.

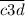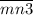2) Числа вида $\overline{c3d}$ и $\overline{mn3}$ . Цифры c и m могут быть любыми из восьми (1,2,4,5,6,7,8,9), а цифры d и n могут быть любыми из девяти (0,1,2,4,5,6,7,8,9). Всего трёхзначных чисел с единственной тройкой в разряде десяток 8·9=72. И столько же с единственной тройкой в разряде единиц 8·9=72.