б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
Запомнив, что х больше либо равен 1, возведем все в квадрат: 16/(х*х)=х-1 x^3-x^2-16=0 Извините, сначала написал неверное решение. У этого кубического уравнения 1 действительный корень х примерно равен 2,901. То что корень примерно равен 3 вытекает из того, что х=3 корень уравнения x^3-x^2-18=0 . Тогда графически нетрудно понять куда смещается корень, когда меняется свободный член. Точное решение ( с формулами Кардано) очень громоздко.
Может быть все же уравнение выглядит так (?): 4/х=sqrt(x)-1 Тогда, очевидно х=4 -решение. Как это получить? Обозначим sqrt(x)=у 4/(у*у)=у-1 y^3-y^2-4=0 (y^3-8)-(y^2-4)=0 (y-2)*(y^2+2y+4)-(y-2)*(y+2)=0 у=2 -решение. Пусть у не равен 2. у^2+y+2=0 (y+0,5)^2+1,75=0 У этого уравнения нет решений. Значит корень один у=2. У исходного уравнения корень х=4.
Смотри решение.
Объяснение:
решения (через дискриминант):
Порядок решения:
а. Записываем уравнение в исходном виде;
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
решения (через теорему Виетта):
Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.
Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.
Общая формула квадратного уравнения: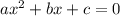
(для справок).
Теперь переходим к решению данного квадратного уравнения:
16/(х*х)=х-1
x^3-x^2-16=0
Извините, сначала написал неверное решение. У этого кубического уравнения 1 действительный корень х примерно равен 2,901.
То что корень примерно равен 3 вытекает из того, что х=3
корень уравнения x^3-x^2-18=0 . Тогда графически нетрудно понять куда смещается корень, когда меняется свободный член.
Точное решение ( с формулами Кардано) очень громоздко.
Может быть все же уравнение выглядит так (?):
4/х=sqrt(x)-1
Тогда, очевидно х=4 -решение.
Как это получить?
Обозначим sqrt(x)=у
4/(у*у)=у-1
y^3-y^2-4=0
(y^3-8)-(y^2-4)=0
(y-2)*(y^2+2y+4)-(y-2)*(y+2)=0
у=2 -решение. Пусть у не равен 2.
у^2+y+2=0
(y+0,5)^2+1,75=0
У этого уравнения нет решений.
Значит корень один у=2.
У исходного уравнения корень х=4.