Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:
Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :
(80-у)*у=1596
80у-у^2=1596
y^2-80y+1596=0
D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:
у1,2=(-b±√D)/2a
y1=(80-)/2*1=(80-4)/2=76/2=38
y2=(80+)/2*1=(80+4)/2=84/2=42
Тогда х1+38=80
х1=80-38=42
х2+42=80
х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м
Объяснение:
здесь надо рассмотреть два случая
1) х-5>0, x>5, тогда |x-5|=x-5 и 1/(х-5) -2<0, (1-2x+10)/(x-5) <0,
(11-2x)/(x-5) <0 , - __(5)+___(5,5)___-___
общее решение x>5,5 (с учетом, что x-5>0)
2) x-5<0, x<5, тогда |x-5|=5-x и получим уравнение:
1/(5-x) -2<0, (1-10+2x)/ (5-x) <0, (2x-9)/ (5-x) <0
-___(4,5)+(5)___- и общее решение
x<4,5 (с учетом, что x-5<0) , объединяем два случая и
ответ: (-Б; 4,5) и (5,5; +Б) (Б- бесконечность)
Объяснение:
Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:
Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :
(80-у)*у=1596
80у-у^2=1596
y^2-80y+1596=0
D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:
у1,2=(-b±√D)/2a
y1=(80-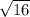
)/2*1=(80-4)/2=76/2=38
y2=(80+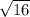
)/2*1=(80+4)/2=84/2=42
Тогда х1+38=80
х1=80-38=42
х2+42=80
х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м