3. не выполняя построения графика функции y = –3x + 4, определите: а) координаты его точек пересечения с осями координат; б) значение функции при х = –2,3; в) значение аргумента, при котором у = –3,5; г) запишите функцию, график которой параллелен графику функции у = –3х + 4 и проходит через точку b(0; 3).

Объяснение:

y= -3x+4.

а) Найдем координаты точек пересечения с осями координат

С осью Оy :  x=0    y=-3*0+4 =4 .

(0;4)- точка пересечения с осью Oy.

С осью Ox: y=0           -3x+4=0;   -3x=-4; x= .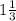

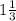(  ;0) - точка пересечения с осью Ox.

б) при x=-2,3       y= -3*(-2,3) +4= 6,9+4=10,9;

в) y= -3,5

г) Если  графики линейных функций параллельны, то их угловые коэффициент равны . Значит для функции y=kx+b   k= -3. Тогда

y= - 3x+b.

Найдем b с учетом ,  что график проходит через точку В (0;3). Подставим координаты этой точки в уравнение, получим:

3= - 3*0+b ;

b=3.

y= - 3x+3.