Найдём производную функции, для нахождения экстремума и промежутков убывания.
1
Найдём минимум этой функции:
Следовательно,
2
Функция убывает там, где .
Т.е. .
Функция убывает на
3
Найдём производную функции, для нахождения экстремума и промежутков убывания.
1
Найдём минимум этой функции:
Следовательно,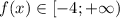
2
Функция убывает там, где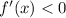 .
.
Т.е.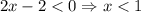 .
.
Функция убывает на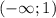
3