4 Бічні сторони | менша основа трапеції мають однакові довжини 50 см. Знайти розмір її більшої основи, при якому площа трапеції була б найбільшою.
З пункту А на прогулянку вийшов пішохід зі швидкістю V км / тод. Після того як він відійшов від А на 6 км, з А слідом за ним виїхав велосипедист, швидкість якого бупа на З км / год більше швидкості пішохода. Коли велосипедист наздогнав пішохода, вони повернули назад повернулися разом в А зі швидкістю 4 км / год. При якому значенні V час прогулянки пішохода виявиться найменшим?
Рассмотрим выражение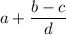
. Чтобы оно было наименьшим, необходимо, чтобы выражения 
и 
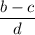были наименьшим.
Заметим, что выражение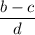
может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит, 
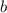необходимо выбрать наименьшим, 
- наибольшим,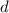 
- наименьшим.
Наибольшее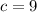
. Наименьшие значения 2, 3, 4 нужно распределить между выражениям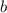и 
, 
и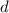 
. Проверим все варианты.
Пусть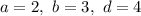
. Тогда: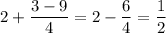 
Пусть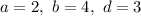
. Тогда: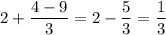 
Пусть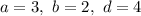
. Тогда: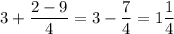 
Пусть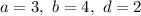
. Тогда: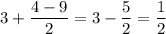 
Пусть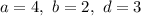
. Тогда: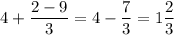 
Пусть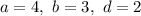
. Тогда: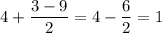 
Наименьшее значение равно 1/3.
ответ: 1/3
0 - не простое число, попарные разности простые => никакая разность не равна 0 => все числа в тройке различны.
Единственное четное простое число - 2. Тогда в тройке по крайней мере 2 нечетных числа => по крайней мере одна разность (как раз этих чисел) будет четной. Т.к. все попарные разности простые, то эта разность равна 2. => тройка имеет вид (a; b; b+2), а разности - |a-b|, |a-b-2|, |b-b-2|=2.
1) Все числа тройки нечетные => все разности четные => все равны 2 => |a-b| = |a-b-2| = 2
a-b=-2 => |a-b-2|=4 - не подходит
a-b=2 => |a-b-2|=0 - не подходит
2) Значит в тройке ровно 2 нечетных числа.
Если b=2, то b+2=4 - не простое.
Если b+2=2, то b=0 - не простое
Тогда a=2 => тройка имеет вид (2; b; b+2), а разности - |2-b|=b-2, |2-b-2|=b, |b-b-2|=2.
Значит b-2, b и b+2 простые. Из чисел такого вида хотя бы одно кратно 3 (b≡0(mod 3)=>b кратно 3, b≡1(mod 3)=>b+2 кратно 3, b≡2(mod 3)=>b-2 кратно 3). Значит какое-то из них равно 3
b-2=3 => b=5, b+2=7 - простые => (2; 5; 7)
b=3 => b-2=1 - не простое
b+2=3 => b=1 - не простое
ответ: (2; 5; 7)