«Молитва это вульгаризованная и рационалистически разжиженная позднейшая форма чего-то очень энергичного, активного и сильного: магического заклинания, принуждения бога» (Т. Манн)
Самая первая, самая красивая, мелодичная часть этой повести – молитва героя. Именно такая молитва, не тихая христианская но убеждение, заклинание, попытка слабого, потерянного человека принудить судьбу измениться. Во имя его любви.
При том, такой любви, в которую очень поверить первой любви, в которой разом встретилась та самая девушка, румяная, взволнованная, очень юная «Она» – и еще весна, цветущие деревья, красота мира, воспринятая молодой, впечатлительной душой, и еще вера в светлое будущее, наивная за него борьба. Все то, что было у него и все, что отняли разом. Сама жизнь, которую он потерял, которую нельзя уже вернуть, но он верит, что можно, с одной единственной нити, с Нее, в образ которой измученно сердце соединило все светлое, что сумело сохранить.
Но Бог, в которого герой никогда прежде не верил, конечно, не внемлет молитве и карает героя за нее, не то чтобы жестоко стирает с лица земли, прекращая разом и надежды и муки. Вообще, у Грина очень интересен мотив «молитвы», она предстает, как заклинание, которое может читать лишь избранный. Для всех же остальных это слабость, непозволительное покушение на божественные сферы. Так и здесь. Молитва сломанного тюрьмой человека, искренняя, жалобная, тихая, у которой недостаточно силы, чтобы заставить Бога покориться человеческой воле.
Сам график не построю, но всё, что нужно для его построения, напишу
Сначала нужно выразить одну переменную через другую:
y - 6x = -25
y = 6x - 25
-y - x = -5
y = 5 - x
Данные функции являются линейными, поэтому их графиками будут прямые, для построения графиков этих функций нужно подставить значение x, и найти при данном значении x значение y (Т.е., к примеру в первой функции при x = 1, y = 6 * 1 - 25 = -19):
y = 6x - 25
Координаты:
x = 1 y = -19
x = 0 y = -25
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
То же самое делаешь и со второй функцией:
y = 5 - x
Координаты:
x = 0 y = 5
x = 1 y = 4
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
Данные прямые пересекутся, и точка их пересечения будет решением системы уравнений
ответом будет и
В связи с таким ответом вопрос: ты точно всё правильно написал?
«Молитва это вульгаризованная и рационалистически разжиженная позднейшая форма чего-то очень энергичного, активного и сильного: магического заклинания, принуждения бога» (Т. Манн)
Самая первая, самая красивая, мелодичная часть этой повести – молитва героя. Именно такая молитва, не тихая христианская но убеждение, заклинание, попытка слабого, потерянного человека принудить судьбу измениться. Во имя его любви.
При том, такой любви, в которую очень поверить первой любви, в которой разом встретилась та самая девушка, румяная, взволнованная, очень юная «Она» – и еще весна, цветущие деревья, красота мира, воспринятая молодой, впечатлительной душой, и еще вера в светлое будущее, наивная за него борьба. Все то, что было у него и все, что отняли разом. Сама жизнь, которую он потерял, которую нельзя уже вернуть, но он верит, что можно, с одной единственной нити, с Нее, в образ которой измученно сердце соединило все светлое, что сумело сохранить.
Но Бог, в которого герой никогда прежде не верил, конечно, не внемлет молитве и карает героя за нее, не то чтобы жестоко стирает с лица земли, прекращая разом и надежды и муки. Вообще, у Грина очень интересен мотив «молитвы», она предстает, как заклинание, которое может читать лишь избранный. Для всех же остальных это слабость, непозволительное покушение на божественные сферы. Так и здесь. Молитва сломанного тюрьмой человека, искренняя, жалобная, тихая, у которой недостаточно силы, чтобы заставить Бога покориться человеческой воле.
«У него была одна молитва, только одна…»
Сам график не построю, но всё, что нужно для его построения, напишу
Сначала нужно выразить одну переменную через другую:
y - 6x = -25
y = 6x - 25
-y - x = -5
y = 5 - x
Данные функции являются линейными, поэтому их графиками будут прямые, для построения графиков этих функций нужно подставить значение x, и найти при данном значении x значение y (Т.е., к примеру в первой функции при x = 1, y = 6 * 1 - 25 = -19):
y = 6x - 25
Координаты:
x = 1 y = -19
x = 0 y = -25
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
То же самое делаешь и со второй функцией:
y = 5 - x
Координаты:
x = 0 y = 5
x = 1 y = 4
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
Данные прямые пересекутся, и точка их пересечения будет решением системы уравнений
ответом будет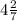 и
и 
В связи с таким ответом вопрос: ты точно всё правильно написал?