5|х-у|=10
3х-7у=20-2|х+у|
все в системе​

Можно решить путем составления системы уравнений. обозначим через х - число деталей в день 1 рабочего, а через у - количество дней. тогда для второго рабочего это будет х+5 и у-1 составим систему { ху=100                                     (х+5)(у-1)=100 преобразуя эту систему, получим у=(х+5)/5. далее в выражение ху=100  подставим значение у. получим квадратное уравнение x^2+5x-500=0. корнями этого уравнения будут х1=-25, х2=20. выбираем 20. столько изготавливает в день первый рабочий.

Правильное условие такое:

У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок? ​

Решение.

ОДЗ: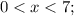    

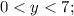
Методом подбора быстрее.

1) Начнем с решения второго уравнения.

Если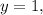 то 7-1=6. Тогда  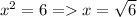не натуральное число.

Если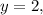 то 7-2=5. Тогда  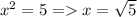не натуральное число.

Если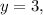 то 7-3=4. Тогда  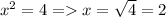натуральное число.

Получили решение

 

2) Подставим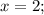 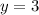     в первое уравнение   .

 

 

        верное равенство.

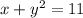ответ: 2 груши у брата;

           3 яблока у сестры.