5. Отношение «х > у» рассматривается на множестве X. Каким бу¬дет его график на координатной плоскости, если: а) X =12,4,6,8}; б) X- множество натуральных чисел; в) А'- множество действительных чисел?
Докажем, что уравнение имеет не более 1 корня. Для этого слагаемое в правой части перенесем в левую часть со знаком минус, 1 - вправо, аналогично со знаком минус:
Функция монотонна возрастающая, а функция - монотонно убывающая для любого значения . Так как сумма монотонно возрастающей и монотонно убывающей функций есть функция монотонно возрастающая, а в правой части - функция постоянная, то графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Делаем вывод: исходное уравнение имеет не более 1 корня, что и требовалось доказать.
Методом подбора легко находим корень . Действительно:
ОТВЕТ: {2}
Поступаем аналогично. В левой части - сумма двух монотонно убывающих функций, а значит функция - монотонно убывающая. Справа имеем постоянную функцию. Следовательно, графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Т.е. исходное уравнение имеет не более 1 корня.
Методом подбора находим все тот же корень . Действительно:
ОТВЕТ: {2}
ОДЗ: |x-3| ≠ 1 ⇒ x ≠ 2; 4.
С учетом ОДЗ неравенство равносильно следующему:
,
Решаем последнее неравенство методом интервалов: на числовой прямой отмечаем все нули функции в левой части (это числа х = 2 и х = 4 для первой скобки, х = 3,5 - для второй и х = 0, но нули выкалываем, так как неравенство строгое).
1. Графики линейной функции, прямая линия.
1) у = 1,5х – 6 х=0 у= -6
у=0 0= 1,5х - 6 -1,5х= -6 х=4
Точки пересечения с осями координат (0; -6) (4; 0)
2) у = – 3х + 2 х=0 у=2
у=0 0= -3х + 2 3х = 2 х=2/3
Точки пересечения с осями координат (0; 2) (2/3; 0)
3) у = 4х х=0 у=0 Нет точек пересечения с осями координат, проходит через точку (0; 0)
1) у = -1/2х х=0 у=0 Нет точек пересечения с осями координат, проходит через точку (0; 0)
2) у = 5х + 1 х=0 у=1
у=0 0=5х + 1 -5х = 1 х= -0,2
Точки пересечения с осями координат (0; 1) (-0,2; 0)
3) у = - 0,25 х – 1 х=0 у= -1
у= 0 0= - 0,25 х – 1 0,25х = -1 х= 4
Точки пересечения с осями координат (0; -1) (4; 0)
2. у = 1,5х – 8,
Для выполнения этого задания нужно подставить значения х и у в уравнение. Если левая часть будет равна правой, проходит, и наоборот.
Для А: -14 = 1,5 * (-40) - 8
-14 = -60 - 8
-14 ≠ -68, не проходит
Для В: 536 = 1,5 * (-352) - 8
536 = -528 - 8
536 ≠ - 536, не проходит.
Докажем, что уравнение имеет не более 1 корня. Для этого слагаемое в правой части перенесем в левую часть со знаком минус, 1 - вправо, аналогично со знаком минус: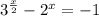
Функция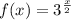 монотонна возрастающая, а функция
монотонна возрастающая, а функция 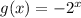 - монотонно убывающая для любого значения
- монотонно убывающая для любого значения  . Так как сумма монотонно возрастающей и монотонно убывающей функций есть функция монотонно возрастающая, а в правой части - функция постоянная, то графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Делаем вывод: исходное уравнение имеет не более 1 корня, что и требовалось доказать.
. Так как сумма монотонно возрастающей и монотонно убывающей функций есть функция монотонно возрастающая, а в правой части - функция постоянная, то графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Делаем вывод: исходное уравнение имеет не более 1 корня, что и требовалось доказать.
Методом подбора легко находим корень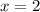 . Действительно:
. Действительно: 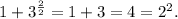
ОТВЕТ: {2}
Поступаем аналогично. В левой части - сумма двух монотонно убывающих функций, а значит функция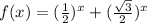 - монотонно убывающая. Справа имеем постоянную функцию. Следовательно, графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Т.е. исходное уравнение имеет не более 1 корня.
- монотонно убывающая. Справа имеем постоянную функцию. Следовательно, графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Т.е. исходное уравнение имеет не более 1 корня.
Методом подбора находим все тот же корень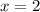 . Действительно:
. Действительно: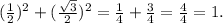
ОТВЕТ: {2}
ОДЗ: |x-3| ≠ 1 ⇒ x ≠ 2; 4.
С учетом ОДЗ неравенство равносильно следующему:
Решаем последнее неравенство методом интервалов: на числовой прямой отмечаем все нули функции в левой части (это числа х = 2 и х = 4 для первой скобки, х = 3,5 - для второй и х = 0, но нули выкалываем, так как неравенство строгое).
Окончательно получаем: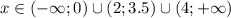 .
.
ОТВЕТ: (-∞; 0) ∪ (2; 3,5) ∪ (4; +∞)