Объяснение:
Задание 5:
Общая для всех формула: a^2 ± 2ab + b^2 = (a±b)^2
1) a^2 - 14a + 49 = (a - 7)^2
2) 25y^2 + 10y + 1 = (5y+1)^2
3) 100a^2 - 180ab + 81b^2 = (10a - 9b)^2
4) 16m^2 + 49n^2 - 56mn = (4m - 7n)^2
5) x^10 - 6x^5b + 9b^2 = (x^5 - 3b)^2
6) 36m^6 + n^12 + 12m^3n^6 = (6m^3 + n^6)^2
Задание 6:
Общая для всех формула: a^2 - b^2 = (a + b)(a - b)
1) x^2 - 25 = (x + 5)(x - 5)
2) 36 - 16y^2 = (6 + 4y)(6 - 4y)
3) 4x^2 - 81y^2 = (2x + 9y)(2x - 9y)
4) 0.09y^2 - 1.21p^2 = (0.3y + 1.1p)(0.3y - 1.1p)
5) a^2b^2 - 16/9 = (ab + 4/3)(ab - 4/3)
6) a^8 - x^4 = (a^4 + x^2)(a^4 - x^2)
7) 0.04b^4 - a^12 = (0.2b^2 + a^6)(0.2b^2 - a^6)
8) -1 + a^6b^4 = (1 + a^3b^2)(1 - a^3b^2)
(Отметье как лучший ответ)
Используем два факта:
1) Если три последовательных числа являются членом арифметической прогрессии, то среднее является средним арифметическим:
2) То же самое с геометрической прогрессией — там средним геометрическим:
Поработаем со вторым уравнением, используя первое:
Первое уравнение нам больше не нужно. Упростим уравнения (2) и (3):
Используем обратную теорему Виета, где второй член равен сумме корней, взятой со знаком минус, а третий член — произведению:
Я сразу по теореме Виета вижу корни: , . Можете решить через дискриминант.
В итоге получили, что либо (ещё из условия было видно, что обе прогрессии симметричны относительно убывания/возрастания).
ответ: 18, 5, 2 либо 2, 5, 18.
Объяснение:
Задание 5:
Общая для всех формула: a^2 ± 2ab + b^2 = (a±b)^2
1) a^2 - 14a + 49 = (a - 7)^2
2) 25y^2 + 10y + 1 = (5y+1)^2
3) 100a^2 - 180ab + 81b^2 = (10a - 9b)^2
4) 16m^2 + 49n^2 - 56mn = (4m - 7n)^2
5) x^10 - 6x^5b + 9b^2 = (x^5 - 3b)^2
6) 36m^6 + n^12 + 12m^3n^6 = (6m^3 + n^6)^2
Задание 6:
Общая для всех формула: a^2 - b^2 = (a + b)(a - b)
1) x^2 - 25 = (x + 5)(x - 5)
2) 36 - 16y^2 = (6 + 4y)(6 - 4y)
3) 4x^2 - 81y^2 = (2x + 9y)(2x - 9y)
4) 0.09y^2 - 1.21p^2 = (0.3y + 1.1p)(0.3y - 1.1p)
5) a^2b^2 - 16/9 = (ab + 4/3)(ab - 4/3)
6) a^8 - x^4 = (a^4 + x^2)(a^4 - x^2)
7) 0.04b^4 - a^12 = (0.2b^2 + a^6)(0.2b^2 - a^6)
8) -1 + a^6b^4 = (1 + a^3b^2)(1 - a^3b^2)
(Отметье как лучший ответ)
Используем два факта:
1) Если три последовательных числа являются членом арифметической прогрессии, то среднее является средним арифметическим:
2) То же самое с геометрической прогрессией — там средним геометрическим:
Поработаем со вторым уравнением, используя первое:
Первое уравнение нам больше не нужно. Упростим уравнения (2) и (3):
Используем обратную теорему Виета, где второй член равен сумме корней, взятой со знаком минус, а третий член — произведению:
Я сразу по теореме Виета вижу корни: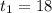
, 
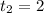. Можете решить через дискриминант.
В итоге получили, чт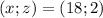о
либо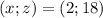 
(ещё из условия было видно, что обе прогрессии симметричны относительно убывания/возрастания).
ответ: 18, 5, 2 либо 2, 5, 18.