График функции у=а(х-m)2+n можно получить из графика функции у = аx2 последовательно выполняя преобразования, которые мы выполняли на предыдущих уроках
2) Отработать умение учащихся по графику описывать свойства квадратичной функции на готовых графиках-тренажёрах:
-Множество значений функции
-Ось симметрии квадратичной функции
-Промежутки убывания функции
-Промежутки возрастания функции
- наименьшее или наибольшее значение функции.
Пример 1. Построить график функции у = (х - 2)2- 3.
Решение. Выполним построение данного графика по этапам.
построения графика функции у = (х - 2)2- 3
1) Построим график функции у = х2 (пунктирная линия).
2) Сдвинув параболу у = х2, на 2 единицы вправо, получим график функции у = (х - 2)2 .
3) Сдвинув параболу у=(х - 2)2 на 3 единицы вниз, получим график функции у=(х - 2)2 - 3 .
Опишите свойства функции у = (х - 2)2 – 3 по графику.
Наше уравнение вида , значит будет проще найти дискриминант по 2 формуле: (где , ).
2. Определим кол-во корней в уравнении.
Вспоминаем правила дискриминанта:
Если дискриминант больше нуля, то уравнение имеет 2 корня.Если дискриминант меньше нуля, то уравнение не имеет корней.Если дискриминант равен нулю, то уравнение имеет 1 корень.
Найденный дискриминант больше нуля , поэтому данное уравнение имеет 2 корня.
График функции у=а(х-m)2+n можно получить из графика функции у = аx2 последовательно выполняя преобразования, которые мы выполняли на предыдущих уроках
2) Отработать умение учащихся по графику описывать свойства квадратичной функции на готовых графиках-тренажёрах:
-Множество значений функции
-Ось симметрии квадратичной функции
-Промежутки убывания функции
-Промежутки возрастания функции
- наименьшее или наибольшее значение функции.
Пример 1. Построить график функции у = (х - 2)2- 3.
Решение. Выполним построение данного графика по этапам.
построения графика функции у = (х - 2)2- 3
1) Построим график функции у = х2 (пунктирная линия).
2) Сдвинув параболу у = х2, на 2 единицы вправо, получим график функции у = (х - 2)2 .
3) Сдвинув параболу у=(х - 2)2 на 3 единицы вниз, получим график функции у=(х - 2)2 - 3 .
Опишите свойства функции у = (х - 2)2 – 3 по графику.
Наше уравнение вида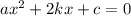 , значит будет проще найти дискриминант по 2 формуле:
, значит будет проще найти дискриминант по 2 формуле: 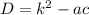 (где
(где 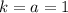 ,
, 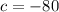 ).
).
Вспоминаем правила дискриминанта:
Если дискриминант больше нуля, то уравнение имеет 2 корня.Если дискриминант меньше нуля, то уравнение не имеет корней.Если дискриминант равен нулю, то уравнение имеет 1 корень.Найденный дискриминант больше нуля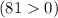 , поэтому данное уравнение имеет 2 корня.
, поэтому данное уравнение имеет 2 корня.
3. Найдём определённое кол-во корней уравнения.Формула корня(-ей) такова: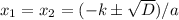
(где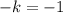 ,
, 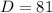 ,
, 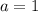 ).
).
Корни данного уравнения: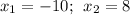 .
.