Введем функции и . Про вторую сразу скажем, что , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это при или . Тогда наименьшее значение этой функции будет равно .
Теперь разберемся с . У нас есть квадратный корень, поэтому все значения функции точно . Но и здесь мы идем дальше. Поменяем временно на букву . Тогда будет . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное при , откуда .
Наибольшее значение равно и достигается при . Наименьшее значение равно и достигается при или .
- 0,8
Объяснение:
1) Выносим cosα за скобки и затем каждый сомножитель приравниваем к 0 ("произведение равно нулю, когда один или оба сомножителя равны нулю").
4cos²α - 3sinα· cosα = 0
cosα · (4cosα - 3sinα) = 0
cosα = 0 - отбрасываем, т.к. cosα = 0, если α = π, а точка π не входит в диапазон, заданный условием задачи (π<α<3π/2).
2) Решаем вторую скобку:
(4cosα - 3sinα) = 0
а) переносим - 3sinα вправо;
4cosα = 3sinα
б) делим обе части на 4, а затем на sinα ≠ 0, получаем:
ctg α = 3/4
3) Находим sinα по формуле:
sinα = 1/(±√(1+ctg²α).
Так как α - угол 3-ей четверти, то ответ будет со знаком минус:
sinα = - 1/(√(1+9/16) = - 1/(5/4) = - 4/5 = -0,8
ответ: - 0,8
(см. объяснение)
Объяснение:
Введем функции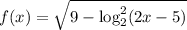 и
и 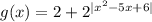 . Про вторую сразу скажем, что
. Про вторую сразу скажем, что 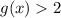 , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 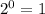 при
при 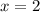 или
или 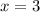 . Тогда наименьшее значение этой функции будет равно
. Тогда наименьшее значение этой функции будет равно 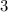 .
.
Теперь разберемся с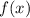 . У нас есть квадратный корень, поэтому все значения функции точно
. У нас есть квадратный корень, поэтому все значения функции точно 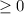 . Но и здесь мы идем дальше. Поменяем временно
. Но и здесь мы идем дальше. Поменяем временно 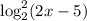 на букву
на букву 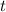 . Тогда будет
. Тогда будет 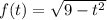 . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное
. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 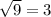 при
при 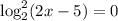 , откуда
, откуда 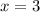 .
.
Наибольшее значение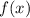 равно
равно 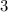 и достигается при
и достигается при 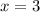 . Наименьшее значение
. Наименьшее значение 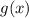 равно
равно 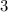 и достигается при
и достигается при 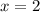 или
или 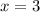 .
.
Тогда единственный корень исходного уравнения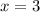 .
.
Уравнение решено!