Давайте сначала обозначим неизвестные. Sв - Расстояние от Вишневого. Sя - Расстояние до Яблоневого. Vв - Cкорость автобуса от Вишневого. Vя - Скорость автомобиля от Яблоневого. Теперь вспоминаем, что все данные должны быть в километрах и часах, а у нас встречаются минуты. Переведем их в часы. 45 минут =45/60 часа или 3/4 часа 45+5=50 минут =50/60 часа или 5/6 часа.
Теперь, учитывая, что скорость автомобиля на 12 км/ч больше скорости автобуса, а расстояние на 14 км больше, напишем выражение для первого расстояния : Sв=3Vв/4 и для второго: Sя=5Vя/6 или Sв+14=5/6 (Vв+12)
Подставим в последне выражение Sв из самого первого:
3Vв/4+14=5/6 (Vв+12)
Раскроем скобки
3Vв/4+14= 5Vв/6+10
Перенесем незвестные в одну сторону, а известные в другую: Vв(3/4-5/6)=10-14 Выполним вычитание дробей, приведя их к одному знаменателю:
Vв(9/12-10/12)=10-14
-Vв/12=-4
Найдем неизвестное: Vв=-4*(-12)=48
Это скорость автобуса.
Скорость автомобиля на 12 больше
Vя=48+12=60 км/ч
Проверим:
48*3/4=36 км 60*5/6=50 км. 50-36=14. Все правильно.
Заметим, что дает такой же остаток при делении на s, что и . (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только )
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Sв - Расстояние от Вишневого.
Sя - Расстояние до Яблоневого.
Vв - Cкорость автобуса от Вишневого.
Vя - Скорость автомобиля от Яблоневого.
Теперь вспоминаем, что все данные должны быть в километрах и часах, а у нас встречаются минуты. Переведем их в часы.
45 минут =45/60 часа или 3/4 часа
45+5=50 минут =50/60 часа или 5/6 часа.
Теперь, учитывая, что скорость автомобиля на 12 км/ч больше скорости автобуса, а расстояние на 14 км больше, напишем выражение для первого расстояния :
Sв=3Vв/4
и для второго:
Sя=5Vя/6 или Sв+14=5/6 (Vв+12)
Подставим в последне выражение Sв из самого первого:
3Vв/4+14=5/6 (Vв+12)
Раскроем скобки
3Vв/4+14= 5Vв/6+10
Перенесем незвестные в одну сторону, а известные в другую:
Vв(3/4-5/6)=10-14
Выполним вычитание дробей, приведя их к одному знаменателю:
Vв(9/12-10/12)=10-14
-Vв/12=-4
Найдем неизвестное:
Vв=-4*(-12)=48
Это скорость автобуса.
Скорость автомобиля на 12 больше
Vя=48+12=60 км/ч
Проверим:
48*3/4=36 км
60*5/6=50 км.
50-36=14. Все правильно.
ответ 48 и 60 км/ч
Заметим, что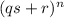
дает такой же остаток при делении на s, что и 
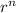. (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только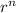
)
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Применяем наблюдения: