Перепишем уравнение, учитывая, что
-----(1)
В уравнение (1) выражение находится в знаменателе, поэтому , или , - целое
или , - целое-----(2)
Сократим в левой части уравнения (1) на :
, отсюда , отсюда
, или , - целое ------(3)
Из решений (3) надо исключить значения, равные значениям (2):
, отсюда
, сокращая на , получим
- нечетные числа
Другими словами принимает только четные значения!
Из условия следует, что , отсюда
Таким образом, принимает значения
Видно, что решения (3) уравнения составляют арифметическую прогрессию с первым членом и последним седьмым членом
Теперь мы можем найти сумму всех решений уравнения как сумму первых семи членов арифметической прогрессии:
sinx * siny = 1/4
cosx * cosy = 3/4
Сложим и вычтем уравнения системы. Получаем
cosx * cosy + sinx * siny = 1
cosx * cosy - sinx * siny = 1/2
cos (x - y) = 1
cos (x + y) = 1/2
x - y = 2 * π * n
x + y = ±π/3 + 2 * π * m
Сложим и вычтем уравнения полученной системы
2 * х = 2 * π * n ± π/3 + 2 * π * m
2 * y = ± π/3 + 2 * π * m - 2 * π * n
x = π * n ± π/6 + π * m
y = ± π/6 + π * m - π * n
или
sinx*siny=1/4
cosx*cosy=3/4
Сложим и вычтем уравнения системы и по формулам косинуса суммы и разности перейдем к более простой системе:
cos(x+y) = 1/2, x+y = +-pi/3 + 2pik
cos(x-y) = 1, x-y = 2pik, вычтем из первого-второе:
Объяснение:
это как я понимаю
Перепишем уравнение, учитывая, что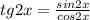
В уравнение (1) выражение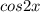 находится в знаменателе, поэтому
находится в знаменателе, поэтому 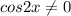 , или
, или 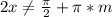 ,
, 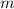 - целое
- целое
или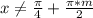 ,
, 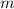 - целое-----(2)
- целое-----(2)
Сократим в левой части уравнения (1) на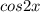 :
:
Из решений (3) надо исключить значения, равные значениям (2):
Другими словами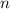 принимает только четные значения!
принимает только четные значения!
Из условия следует, что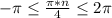 , отсюда
, отсюда
Таким образом,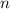 принимает значения
принимает значения 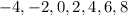
Видно, что решения (3) уравнения составляют арифметическую прогрессию с первым членом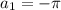 и последним седьмым членом
и последним седьмым членом
Теперь мы можем найти сумму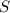 всех решений уравнения как сумму первых семи членов арифметической прогрессии:
всех решений уравнения как сумму первых семи членов арифметической прогрессии:
sinx * siny = 1/4
cosx * cosy = 3/4
Сложим и вычтем уравнения системы. Получаем
cosx * cosy + sinx * siny = 1
cosx * cosy - sinx * siny = 1/2
cos (x - y) = 1
cos (x + y) = 1/2
x - y = 2 * π * n
x + y = ±π/3 + 2 * π * m
Сложим и вычтем уравнения полученной системы
2 * х = 2 * π * n ± π/3 + 2 * π * m
2 * y = ± π/3 + 2 * π * m - 2 * π * n
x = π * n ± π/6 + π * m
y = ± π/6 + π * m - π * n
или
sinx*siny=1/4
cosx*cosy=3/4
Сложим и вычтем уравнения системы и по формулам косинуса суммы и разности перейдем к более простой системе:
cos(x+y) = 1/2, x+y = +-pi/3 + 2pik
cos(x-y) = 1, x-y = 2pik, вычтем из первого-второе:
Объяснение:
это как я понимаю