1) Найти уравнение стороны ВС, её нормальный вектор и угловой коэффициент. , это уравнение в каноническом виде. Знаменатели в этом уравнении - это координаты направляющего вектора: направляющий вектор . Чтобы найти угловой коэффициент, надо уравнение из канонического вида преобразовать в уравнение с коэффициентом: -6х + 42 = -8у - 48, 6х - 8у - 90 = 0 или, сократив на 2: 3х - 4у - 45 = 0 это общий вид уравнения. Теперь выразим относительно у: у = (3/4)х - (45/4) это уравнение с коэффициентом . Угловой коэффициент уравнения стороны равен ВС 3/4. Его можно определить по координатам точек: Квс = (Ус-Ув) / (Хс-Хв). Если прямая задана общим уравнением в прямоугольной системе координат, то вектор является вектором нормали данной прямой. Нормальный вектор (3;-4).
2) Найти точку пересечения медианы, опущенной из вершины А, и высоты, опущенной из вершины В. Для этого надо найти уравнения этих прямых и решить полученную систему. Находим координаты точки М (основание медианы АМ) как середину стороны ВС: М((7-1)/2=3; (-6-12)/2=-9. Отсюда находим уравнение медианы АМ: Находим уравнение высоты из точки В(7;-6) как перпендикуляра (нормали) к стороне АС.
Уравнение
Или в общем виде
Нормальный вектор стороны АС , а для высоты ВН он будет направляющим:
Уравнение высоты
Или в общем виде: -х + 7 = 7у + 42,
х + 7у + 35 = 0.
3) Уравнение прямой, проходящей через точку А параллельно стороне ВС имеет вид 3х - 4у - С = 0, так как уравнение ВС: 3х - 4у - 45 = 0. Подставим координаты точки А: 3*1 - 4*2 - С = 0, отсюда С = 3-8 = -5. Тогда искомое уравнение 3х - 4у + 5 = 0.
Очевидно, задача сводится к тому, чтобы доказать, что при любых а выражение а³-а разделится на 2 и на 3
1. а³ - а = а × а × а - а если а - четное, то а³ - а тоже четное если а - нечетное, то а³ - нечетное. Если из любого нечетного вычесть нечетное, то результат будет четным. Действительно: пусть х - четное и у - четное. Тогда х + 1 - нечетное и у + 1 - нечетное. (х + 1) - (у + 1) = х + 1 - у - 1 = х - у - четное по определению Таким образом, а³ - а - делится на 2 при любых а.
2. а³ - а = а(а² -1) = а(а - 1)(а + 1) - при любом а данное произведение является произведением трех последовательных чисел (а -1) ; а ; (а + 1) Из любых трех последовательных чисел одно всегда разделится на 3, следовательно и все произведение этих чисел разделится на 3
Таким образом, мы доказали, что выражение а³ - а делится на 2 и на 3. Следовательно оно разделится на 6
1) Найти уравнение стороны ВС, её нормальный вектор и угловой коэффициент.
это уравнение в каноническом виде.
Знаменатели в этом уравнении - это координаты направляющего вектора: направляющий вектор
Чтобы найти угловой коэффициент, надо уравнение из канонического вида преобразовать в уравнение с коэффициентом:
-6х + 42 = -8у - 48,
6х - 8у - 90 = 0 или, сократив на 2:
3х - 4у - 45 = 0 это общий вид уравнения.
Теперь выразим относительно у:
у = (3/4)х - (45/4) это уравнение с коэффициентом .
Угловой коэффициент уравнения стороны равен ВС 3/4.
Его можно определить по координатам точек:
Квс = (Ус-Ув) / (Хс-Хв).
Если прямая задана общим уравнением
Нормальный вектор (3;-4).
2) Найти точку пересечения медианы, опущенной из вершины А, и высоты, опущенной из вершины В.
Для этого надо найти уравнения этих прямых и решить полученную систему.
Находим координаты точки М (основание медианы АМ) как середину стороны ВС: М((7-1)/2=3; (-6-12)/2=-9.
Отсюда находим уравнение медианы АМ:
Находим уравнение высоты из точки В(7;-6) как перпендикуляра (нормали) к стороне АС.
Уравнение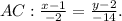
Или в общем виде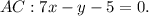
Нормальный вектор стороны АС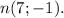 , а для высоты ВН он будет направляющим:
, а для высоты ВН он будет направляющим:
Уравнение высоты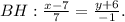
Или в общем виде: -х + 7 = 7у + 42,
х + 7у + 35 = 0.
3) Уравнение прямой, проходящей через точку А параллельно стороне ВС имеет вид 3х - 4у - С = 0, так как уравнение ВС: 3х - 4у - 45 = 0.Подставим координаты точки А: 3*1 - 4*2 - С = 0, отсюда С = 3-8 = -5.
Тогда искомое уравнение 3х - 4у + 5 = 0.
1. а³ - а = а × а × а - а
если а - четное, то а³ - а тоже четное
если а - нечетное, то а³ - нечетное. Если из любого нечетного вычесть
нечетное, то результат будет четным.
Действительно: пусть х - четное и у - четное. Тогда х + 1 - нечетное и
у + 1 - нечетное.
(х + 1) - (у + 1) = х + 1 - у - 1 = х - у - четное по определению
Таким образом, а³ - а - делится на 2 при любых а.
2. а³ - а = а(а² -1) = а(а - 1)(а + 1) - при любом а данное произведение является произведением трех последовательных чисел (а -1) ; а ; (а + 1)
Из любых трех последовательных чисел одно всегда разделится на 3, следовательно и все произведение этих чисел разделится на 3
Таким образом, мы доказали, что выражение а³ - а делится на 2 и на 3. Следовательно оно разделится на 6