Чтобы упростить выражение (4а + 3b)^2 - (2a - b)(5a - 9b) откроем скобки и приведем подобные слагаемые.
Для открытия скобок будем использовать формулу сокращенного умножения квадрат суммы (a + b)^2 = a^2 + 2ab + b^2, правило умножения скобки на скобку и правило открытия скобки перед которой стоит знак минус.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть , где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
Чтобы упростить выражение (4а + 3b)^2 - (2a - b)(5a - 9b) откроем скобки и приведем подобные слагаемые.
Для открытия скобок будем использовать формулу сокращенного умножения квадрат суммы (a + b)^2 = a^2 + 2ab + b^2, правило умножения скобки на скобку и правило открытия скобки перед которой стоит знак минус.
(4а + 3b)^2 - (2a - b)(5a - 9b) = (4а)^2 + 2 * 4a * 3b + (3b)^2 - (2a * 5a - 2a * 9b - 5a * b - b * (- 9b)) = 16a^2 + 24ab + 9b^2 - (10a^2 - 18ab - 5ab + 9b^2) = 16a^2 + 24ab + 9b^2 - 10a^2 + 18ab + 5ab - 9b^2 = 16a^2 - 10a^2 + 9b^2 - 9b^2 + 24ab + 18ab + 5ab = 6a^2 + 47ab.
ответ: 6a^2 + 47ab.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть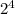
, где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов: