а) две точки пересечения (два корня)
b)
Объяснение:
a) в) окружность R=3, O(0;0) и
парабола с ветвями вниз, вершина(0;4)
четыре точки симметричные относительно
оси "y"
б) xy=3 или гипербола, точка симметрии (0;0)
окружность R=2 центр (0,0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы и
у окружности и
г) это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.
Дано:
A) x⁴ + x³ + 11x² + 6x - 12
B) x⁴ + x³ - 7x² - x + 6
C) x⁴ - x³ - x² + 7x - 6
D) x⁴ - x³ - 11x² + 6x - 8
Корни многочлена
x₁ = -1
x₂ = 1
x₃ = 2
x₄ = -3
Найти:
Выбрать многочлен с данными корнями
Многочлен А)
Подставим корень x₁ = -1
(-1)⁴ + (-1)³ + 11 · (-1)² + 6 · (-1) - 12 = 1 - 1 + 11 - 6 -12 = -7
Многочлен А) не подходит, так как его значение при x₁ = -1 не равно нулю.
Многочлен В)
(-1)⁴ + (-1)³ - 7 · (-1)² - (-1) + 6 = 1 - 1 - 7 + 1 + 6 =0
Продолжим проверку
Подставим корень x₂ = 1
1⁴ + 1³ - 7 · 1² - 1 + 6 = 1 + 1 - 7 - 1 + 6 = 0
Подставим корень x₃ = 2
2⁴ + 2³ - 7 · 2² - 2 + 6 = 16 + 8 - 28 - 2 + 6 = 0
Проверим и последний корень
(-3)⁴ + (-3)³ - 7 · (-3)² - (-3) + 6 = 81 - 27 - 63 + 3 + 6 = 0
Многочлен В) подходит, так как его значение при ПРИ ВСЕХ КОРНЯХ равно нулю.
Многочлен С)
(-1)⁴ - (-1)³ - (-1)² + 7 · (-1) - 6 = 1 + 1 - 1 - 7 - 6 = -12
Многочлен С) не подходит, так как его значение при x₁ = -1 не равно нулю.
Многочлен D)
(-1)⁴ - (-1)³ - 11 · (-1)² + 6 · (-1) - 8 = 1 + 1 - 11 - 6 - 8 = -23
Многочлен D) не подходит, так как его значение при x₁ = -1 не равно нулю.
а) две точки пересечения (два корня)
b)
Объяснение:
a)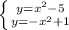
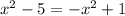 в)
в) 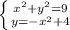 окружность R=3, O(0;0) и
окружность R=3, O(0;0) и
б) xy=3 или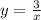 гипербола, точка симметрии (0;0)
гипербола, точка симметрии (0;0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы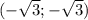 и
и 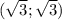
у окружности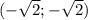 и
и 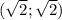
г)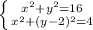 это две окружности: одна R=4, центр (0;0)
это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.
Дано:
A) x⁴ + x³ + 11x² + 6x - 12
B) x⁴ + x³ - 7x² - x + 6
C) x⁴ - x³ - x² + 7x - 6
D) x⁴ - x³ - 11x² + 6x - 8
Корни многочлена
x₁ = -1
x₂ = 1
x₃ = 2
x₄ = -3
Найти:
Выбрать многочлен с данными корнями
Многочлен А)
Подставим корень x₁ = -1
(-1)⁴ + (-1)³ + 11 · (-1)² + 6 · (-1) - 12 = 1 - 1 + 11 - 6 -12 = -7
Многочлен А) не подходит, так как его значение при x₁ = -1 не равно нулю.
Многочлен В)
Подставим корень x₁ = -1
(-1)⁴ + (-1)³ - 7 · (-1)² - (-1) + 6 = 1 - 1 - 7 + 1 + 6 =0
Продолжим проверку
Подставим корень x₂ = 1
1⁴ + 1³ - 7 · 1² - 1 + 6 = 1 + 1 - 7 - 1 + 6 = 0
Продолжим проверку
Подставим корень x₃ = 2
2⁴ + 2³ - 7 · 2² - 2 + 6 = 16 + 8 - 28 - 2 + 6 = 0
Проверим и последний корень
x₄ = -3
(-3)⁴ + (-3)³ - 7 · (-3)² - (-3) + 6 = 81 - 27 - 63 + 3 + 6 = 0
Многочлен В) подходит, так как его значение при ПРИ ВСЕХ КОРНЯХ равно нулю.
Многочлен С)
Подставим корень x₁ = -1
(-1)⁴ - (-1)³ - (-1)² + 7 · (-1) - 6 = 1 + 1 - 1 - 7 - 6 = -12
Многочлен С) не подходит, так как его значение при x₁ = -1 не равно нулю.
Многочлен D)
Подставим корень x₁ = -1
(-1)⁴ - (-1)³ - 11 · (-1)² + 6 · (-1) - 8 = 1 + 1 - 11 - 6 - 8 = -23
Многочлен D) не подходит, так как его значение при x₁ = -1 не равно нулю.
B) x⁴ + x³ - 7x² - x + 6