и множество натуральных чисел ℕ. Замечу, что при любом k дробь вида является несократимой, то есть если выписывать такие дроби, начиная с k = 1 и увеличивая каждый раз переменную k на 1, ни одна из них не повторится (так как знаменатель постоянно увеличивается).
Покажем, что между этими двумя множествами можно установить взаимно однозначное соответствие. Для этого всем дробям вида , где , поставим в соответствие число . С одной стороны, согласно построению каждой такой дроби будет соответствовать натуральное , притом единственное. С другой стороны, для каждого натурального можно указать единственную (смотри замечание в предыдущем абзаце) дробь вида , и все они будут принадлежать множеству A, поскольку пробегает все натуральные значения. Итак, построенное соответствие действительно взаимно однозначное. А раз множество ℕ счетное, то и множество A также счетное.
Пусть х км/ч - скорость туриста от посёлка до речки, (х - 10) км/ч - скорость на обратном пути. 18 мин = (18 : 60) ч = 0,3 ч. Уравнение:
60/(х-10) - 60/х = 0,3
60 · х - 60 · (х - 10) = 0,3 · х · (х - 10)
60х - 60х + 600 = 0,3х² - 3х
600 = 0,3х² - 3х
0,3х² - 3х - 600 = 0
D = b² - 4ac = (-3)² - 4 · 0,3 · (-600) = 9 + 720 = 729
√D = √729 = 27
х₁ = (3-27)/(2·0,3) = -24 : 0,6 = -40 (не подходит, так как < 0)
х₂ = (3+27)/(2·0,3) = 30 : 0,6 = 50 км/ч - скорость от посёлка к речке
50 - 10 = 40 км/ч - скорость от речки к посёлку
60 : 40 = 1,5 ч - время в пути
ответ: 1 час 30 мин турист ехал от речки к посёлку.
Рассмотрим множество A, заданное в условии:
и множество натуральных чисел ℕ. Замечу, что при любом k дробь вида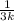
является несократимой, то есть если выписывать такие дроби, начиная с k = 1 и увеличивая каждый раз переменную k на 1, ни одна из них не повторится (так как знаменатель постоянно увеличивается).
Покажем, что между этими двумя множествами можно установить взаимно однозначное соответствие. Для этого всем дробям вида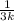
, где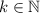 
, поставим в соответствие число 
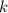. С одной стороны, согласно построению каждой такой дроби будет соответствовать натуральное 
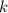, притом единственное. С другой стороны, для каждого натурального 
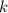можно указать единственную (смотри замечание в предыдущем абзаце) дробь вида 
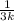, и все они будут принадлежать множеству A, поскольку 
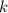пробегает все натуральные значения. Итак, построенное соответствие действительно взаимно однозначное. А раз множество ℕ счетное, то и множество A также счетное.