Разность косинусов:
Рассмотрим уравнение:
Учитывая нечетность функции синуса, получим:
Вынесем общий множитель за скобки:
Произведение равно нулю когда хотя бы один из множителей равен нулю:
ответ:
Фото
Объяснение:
Разность косинусов:
Рассмотрим уравнение:
Учитывая нечетность функции синуса, получим:
Вынесем общий множитель за скобки:
Произведение равно нулю когда хотя бы один из множителей равен нулю:
ответ: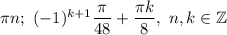
Фото
Объяснение: