Очевидно что данная последовательность представляет собой
арифметическую прогрессию, так как каждое число начинаемое со второго 12,14,....,96,98 образовано из предыдущего числа добавлением к нему шага прогрессии(равного 2)
на краях этого отрезка (x=-п/2 , x=п/2) cos x = 0 - Функция НЕинтегрируема
Б) [0 ; п ]
в середине этого отрезка (x=п/2) cos x = 0 - Функция НЕинтегрируема
В) [-п/4 ; 2п ]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
Г) [п/4 ; 2п]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
ответ: Функция НЕинтегрируема ни на каком отрезке.
Хотя, возможно, имеется в виду теорема о том, что
Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Формально под эту теорему подпадает случай А).
(Но что делать с границами отрезка? Если бы вместо отрезка был интервал (-п/2;п/2), то на этом интервале функция была бы интегрируема в любой точке, и вопросов бы не было и интеграл по интервалу можно было рассматривать, как предельные переходы к границам интервала.
Можно конечно, так же считать и для отрезка [-п/2;п/2], но это очень сомнительное допущение.)
Запишем члены этого ряда
10, 12, 14, ......., 96, 98
Первый член ряда a₁ = 10
Второй член ряда a₂ = 12 и так далее.
Последний член ряда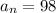
Очевидно что данная последовательность представляет собой
арифметическую прогрессию, так как каждое число начинаемое со второго 12,14,....,96,98 образовано из предыдущего числа добавлением к нему шага прогрессии(равного 2)
Так 12 = 10 + 2, 14 = 12 + 2,....., 98 = 96 + 2
Определим шаг или разность прогрессии - d
d = a₂ - a₁ = 12 - 10 = 2
и количество ее членов прогрессии n из формулы
Найдем сумму n членов арифметической прогрессии
а₁ = 10, d = 2, n = 45
по формуле
ответ: 2430
Функция интегрируема, если cos x не равен нулю.
Функция неинтегрируема, если cos x =0.
cos x = 0 при x = п/2 + пk
Проверяем
A) [-п/2 ; п/2]
на краях этого отрезка (x=-п/2 , x=п/2) cos x = 0 - Функция НЕинтегрируема
Б) [0 ; п ]
в середине этого отрезка (x=п/2) cos x = 0 - Функция НЕинтегрируема
В) [-п/4 ; 2п ]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
Г) [п/4 ; 2п]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
ответ: Функция НЕинтегрируема ни на каком отрезке.
Хотя, возможно, имеется в виду теорема о том, что
Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Формально под эту теорему подпадает случай А).
(Но что делать с границами отрезка? Если бы вместо отрезка был интервал (-п/2;п/2), то на этом интервале функция была бы интегрируема в любой точке, и вопросов бы не было и интеграл по интервалу можно было рассматривать, как предельные переходы к границам интервала.
Можно конечно, так же считать и для отрезка [-п/2;п/2], но это очень сомнительное допущение.)
Так что ответ может быть и А).