Доказать, что многочлен f(x,y,z) = x3+y3+z3 - xyz
нельзя представить в виде произведения многочленов
первой степени с действительными коэффициентами.

Пусть дан многочлен:

Предположим, что его можно представить в виде произведения многочленов  первой степени с действительными коэффициентами.

Многочлен первой степени имеет вид:

, где - cвободный член.

Поскольку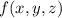 не содержит свободного члена, то хотя бы один из свободных членов в одном из множителей равен .

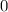Но тогда, существует такая линейная комбинация:

При которой данный многочлен тождественно равен .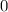

Попробуем найти такую комбинацию:

Мы пришли к противоречию, это невозможно.