Объяснение:
Необходимо доказать, что
Докажем это утверждение с метода математической индукции.
1. База индукции - при n = 1
1² = 1
Получили верное равенство, следовательно база индукции выполнена.
2. Шаг индукции. Предположим, что наше утверждение верно при n = k, т.е.
Докажем теперь, что в таком случае утверждение будет верно и для n = k + 1.
Вместо k² в правую часть равенства подставим верное равенство (1), получим:
Т.е утверждение верно и для n = k + 1 и доказан шаг индукции.
Объяснение:
Необходимо доказать, что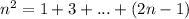
Докажем это утверждение с метода математической индукции.
1. База индукции - при n = 1
1² = 1
Получили верное равенство, следовательно база индукции выполнена.
2. Шаг индукции. Предположим, что наше утверждение верно при n = k, т.е.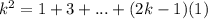
Докажем теперь, что в таком случае утверждение будет верно и для n = k + 1.
Вместо k² в правую часть равенства подставим верное равенство (1), получим:
Т.е утверждение верно и для n = k + 1 и доказан шаг индукции.