Докажите, что не зависит от допустимых значений переменной значение выражения:

Показать ответ

Ответ:

СергейРовкин

19.03.2021 17:41

А) являются (значение суммы при перестановке слагаемых не меняется)
Б) являются. а-1+а+6=2а+5
В) являются (значение суммы при перестановке слагаемых не меняется)
Г) являются. 2(3х-1)=6х-2
Д) являются. х+у-2х+3у=4у-х
Е) являются. -3в+3в=0. 2а=2а
Ж) являются. 3х+5х+4х=12х
З) являются 5х+х-2у=6х-2у
И) являются 2(х^2+у)-х^2=2х^2-х^2+2у
К) не являются. При раскрытии скобок получаются неравные выражения
Л) не являются. При раскрытии скобок получаются неравные выражения
М) не являются. При раскрытии скобок получаются неравные выражения

0,0(0 оценок)

Ответ:

Turtygin

08.04.2021 15:54

Обратную матрицу найдем по формуле:

$A^{-1}=\frac{1}{|A|}*\tilde{A^{T}}$ ,

где |A| - определитель матрицы, а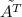 $\tilde{A^{T}}$ - транспонированная матрица алгебраических дополнений

$|A|=\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]=-2+27-5-3-30-3=-16$

Т.к. определитель матрицы не равен 0, то обратная матрица существует.

Находим матрицу миноров. Для каждого элемента матрицы соответствующий ему минор вычисляется по определителю матрицы 2х2, которая получается вычеркиванием соответствующей строки и столбца для этого элемента:

$m_{11}=\left[\begin{array}{cc}-1&3\\5&1\end{array}\right]=-1-15=-16\\m_{12}=\left[\begin{array}{cc}1&3\\3&1\end{array}\right]=1-9=-8\\m_{13}=\left[\begin{array}{cc}1&-1\\3&5\end{array}\right]=5+3=8$

$m_{21}=\left[\begin{array}{cc}3&-1\\5&1\end{array}\right]=3+5=8\\m_{22}=\left[\begin{array}{cc}2&-1\\3&1\end{array}\right]=2+3=5\\m_{23}=\left[\begin{array}{cc}2&3\\3&5\end{array}\right]=10-9=1$

$m_{31}=\left[\begin{array}{cc}3&-1\\-1&3\end{array}\right]=9-1=8\\m_{32}=\left[\begin{array}{cc}2&-1\\1&3\end{array}\right]=6+1=7\\m_{33}=\left[\begin{array}{cc}2&3\\1&-1\end{array}\right]=-2-3=-5$

Получили следующую матрицу миноров:

$M=\left[\begin{array}{ccc}-16&-8&8\\8&5&1\\8&7&-5\end{array}\right]$

Из матрицы миноров получим матрицу алгебраических дополнений заменой знака на противоположный у элементов матрицы миноров, у которых сумма номеров строк и столбца нечетна:

$\tilde{A}=\left[\begin{array}{ccc}-16&8&8\\-8&5&-1\\8&-7&-5\end{array}\right]$

Следующим шагом получаем транспонированную матрицу алгебраических дополнений:

$\tilde{A^T}=\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]$

Обратная матрица:

$A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]$

Проверим, что произведение исходной и обратной матрицы равно единичной:

$A*A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]=-\frac{1}{16}*\left[\begin{array}{ccc}-16&0&0\\0&-16&0\\0&0&-16\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]$