Докажите,что выражение -y^2+2y-8 при любых значениях y принимает отрицательные значения.

Показать ответ

Ответ:

alinaochirovg19

12.05.2020 10:55

1)В прямоугольник вписать окружность нельзя. Это можно сделать только если в четырёхугольнике суммы противоположных сторон равны.

2)В равностороннем треугольнике все стороны равны у все углы по 60 градусов. Пусть стороны будут по 1 см. Тогда 1²+1²=2≠ третьей стороне(1).Приведённое свойство верно только для прямоугольных треугольников (теорема Пифагора).

3)Нет, например: 5+(-3)=2 .

4) В равнобедренном треугольнике все углы могут быть острые. Например, равносторонний треугольник- это частный случай равнобедренного треугольника. Там все углы по 60 градусов. Или в равнобедренном прямоугольном треугольнике углы равны 90⁰, 45⁰,45⁰.

0,0(0 оценок)

Ответ:

DenGamer11

16.05.2020 23:00

Во всех случаях исходов будет n = 6*6 = 36

1) Положительных исходов у нас m =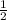 $\frac{1}{2}$ (n - исходы, когда выпало одинаковое количество очков)

$m = \frac{36 - 6}{2} = 15$

$p = \frac{m}{n} = \frac{15}{36}$

2) Сумму пять можно получить так: 1+4, 2+3, 3+2, 4+1.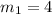 m_1 = 4

Сумму шесть можно получить так: 1+5, 2+4, 3+3, 4+2, 5+1.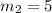 m_2 = 5

$p_1 = \frac{m_2}{n} = \frac{5}{36} p_2 = \frac{4}{36}$

Выпадение суммы равной шести более вероятно, чем выпадение пяти.

3) Очевидно, что у нас имеется 36 возможных сумм, часть из которых совпадает. Меньше всего будет встречаться 2 (1+1) и 12 (6+6), чаще всего 7 (1+6, 2+5, 3+4, 4+3, 5+2, 6+1)

2 (1+1)

3 (1+2, 2+1)

4 (1+3, 2+2, 3+1)

5 (1+4, 2+3, 3+2, 4+1)

6 (1+5, 2+4, 3+3, 4+2, 5+1)

7 (1+6, 2+5, 3+4, 4+3, 5+2, 6+1)

8 (2+6, 3+5, 4+4, 5+3, 6+2)

9 (3+6, 4+5, 5+4, 6+3)

10 (4+6, 5+5, 6+4)

11 (5+6, 6+5)

12 (6+6)

0,0(0 оценок)