Поясняю. Второй график сразу узнаете, т.к. единственный из них, который ветвями вниз, и это указывает на коэффициент, равный -1
Первый и третий похожи, но по формуле для абсциссы вершины параболы найдем для первого графика функции -в/2а = 5/2=2.5, сразу виден график В, а для третьего -в/2а = -5/2=-2.5, остальное просто проверяется на автомате. т.е. оба направлены ветвями вверх, как А так и В, и точки пересечения с осью ОУ у них одинаковы, т.к. отличаются только вторым коэффициентом.
Её можно получить из графика гиперболы путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
ответ 1-В; 2-Б; 3-А.
Поясняю. Второй график сразу узнаете, т.к. единственный из них, который ветвями вниз, и это указывает на коэффициент, равный -1
Первый и третий похожи, но по формуле для абсциссы вершины параболы найдем для первого графика функции -в/2а = 5/2=2.5, сразу виден график В, а для третьего -в/2а = -5/2=-2.5, остальное просто проверяется на автомате. т.е. оба направлены ветвями вверх, как А так и В, и точки пересечения с осью ОУ у них одинаковы, т.к. отличаются только вторым коэффициентом.
Графиком функции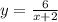 является гипербола.
является гипербола.
Её можно получить из графика гиперболы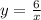 путём сдвига на 2 единицы влево вдоль оси ОХ.
путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
у(наибол)=у(0)=3 , у(наимен)=у(4)=1
На области определения функция убывающая.